Ingin mempelajari materi kimia, khususnya tentang Hukum Gas Van der Waals & Gas Graham? Supaya lebih paham, kamu bisa menyimak pembelajarannya di sini. Kamu juga bisa mengerjakan soal latihan untuk mempraktikkan materi yang telah dijelaskan.
Lewat pembahasan ini, kamu bisa belajar mengenai Hukum Gas Van der Waals & Gas Graham. kamu akan diajak untuk memahami materi dan tentang metode menyelesaikan soal.
Kamu juga akan memperoleh latihan soal interaktif yang tersedia dalam tiga tingkat kesulitan, yaitu mudah, sedang, dan sukar. Tertarik untuk mempelajarinya?
Sekarang, kamu bisa mulai mempelajari materi lewat uraian berikut. Apabila materi ini berguna, bagikan ke teman-teman kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & contoh soal serta kumpulan latihan soal Hukum Gas Van der Waals & Gas Graham dalam bentuk pdf pada link dibawah ini:
Definisi
Pengertian hukum van der Waals atau gas nyata merumuskan perilaku gas non-ideal (gas nyata).
Hukum Graham menyatakan bahwa laju efusi suatu gas berbanding terbalik dengan akar dari massa molarnya.
Penulisan Waals mengunakan awalan huruf besar karena merupakan nama tokoh penemu hukum gas nyata yakni Johannes van der Waals, juga dengan nama Graham.
Hukum Gas Van der Waals (Gas Nyata)
Dari data-data yang dikumpulkan mengenai gas-gas nyata, diketahui bahwa terdapat penyimpangan terhadap perilaku gas ideal. Seperti terlihat pada grafik berikut ini, dimana diplot nilai $\frac{PV}{RT}$ terhadap P untuk tiap mol beberapa gas.
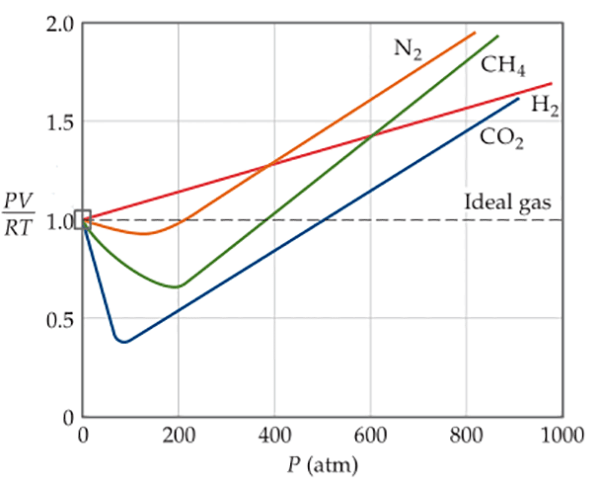
Untuk suatu gas ideal, seharusnya nilai $\frac{PV}{RT}$ konstan pada 1,00 bila digunakan 1,00 mol gas sesuai persamaan gas ideal. Perilaku non-ideal ini dapat dijelaskan sebagai berikut. Hukum Boyle memprediksi bahwa, pada tekanan yang sangat tinggi, volume suatu gas menjadi sangat kecil dan mendekati nol.
Tentunya hal ini tidak mungkin terjadi, karena molekul-molekul gas tersebut menempati ruang, yang tidak dapat dikompresi lebih lanjut. Sehingga nilai $PV$ pada temperatur tinggi akan bernilai lebih tinggi dari 1.
Selain itu, penyimpangan ini terjadi karena adanya interaksi intermolekuler antara molekul gas, sehingga gaya tumbukan antara molekul gas dengan dinding wadah menjadi lebih rendah dibanding yang diharapkan (gas ideal).
Karena gaya tumbukan menjadi lebih lemah Interaksi ini akan makin kuat pada temperatur rendah, karena pergerakan molekul gas yang lambat.
Apabila dirangkum:
- Suatu gas akan bersifat paling ideal pada suhu tinggi dan tekanan rendah
- Suatu gas akan bersifat paling non-ideal pada suhu rendah dan tekanan tinggi
Pada kondisi non-ideal, atau disebut juga untuk gas nyata, kita dapat menggunakan persamaan gas nyata atau persamaan van der waals berikut:
$\left(P+\frac{an^{2}}{V^{2}}\right)\left(V-nb\right)=nRT$
Dimana a dan b adalah konstanta van der Waals dengan nilai yang berbeda untuk setiap molekul gas, yang dapat dirangkum sebagai berikut:

Konstanta a disebut juga konstanta proporsionalitas yang menunjukkan kuatnya interaksi intermolekuler antar molekul gas tersebut. Sementara konstanta b menunjukkan pengaruh dari volume molekul gas itu sendiri.
Hukum Gas Graham
Pada 1846, ilmuan bernama Thomas Graham mengemukakan bahwa laju efusi suatu gas berbanding terbalik dengan akar dari massa molarnya. Bila laju efusi dua jenis gas dilambangkan dengan $r_{1}$ dan $r_{2}$ sementara massa molarnya adalah $M_{1}$ dan $M_{2}$, maka persamaan Hukum Graham adalah :
$\frac{r_{1}}{r_{2}}=\sqrt{\frac{M_{2}}{M_{1}}}$
Hukum Graham laju molekul gas dapat diturunkan sebagai berikut: laju suatu molekul gas dirumuskan sebagai kecepatan root mean square nya, maka didapat persamaan berikut:
$\frac{r_{1}}{r_{2}}=\frac{\mu_{rms1}}{\mu_{rms2}}=\sqrt{\frac{3RT/M_{1}}{3RT/M_{2}}}$
maka, pada kondisi temperatur yang sama, nilai $3RT$ konstan, sehingga didapat persamaan hukum Graham.
Namun harus diperhatikan bahwa Hukum Graham memiliki beberapa keterbatasan, antara lain ia hanya berlaku untuk sistem pada tekanan rendah, dimana efusi terjadi pada satu per satu molekul gas, bukan dalam jumlah yang besar.
Selain itu hukum ini juga tidak berlaku untuk difusi karena pada proses difusi molekul gas saling bertumbukan satu sama lain, sehingga secara kuantitatif persamaan Graham tidak dapat digunakan untuk difusi.
Secara umum, Hukum Graham dapat digunakan untuk menghitung rasio dari
- laju molekul
- laju efusi
- waktu efusi
- jarak yang ditempuh molekul gas
- jumlah gas yang berefusi
yang sama besar dengan akar dari rasio massa molekul gas yang dibandingkan.
Contoh Soal Hukum Gas Van der Waals & Gas Graham dan Pembahasannya
Apabila 71 g gas klorin ditempatkan di dalam wadah dengan volume 2,00 L pada 273 K, tentukan tekanan nyatanya! (konstanta v.d.W : $a=6,49L^{2}atmmol^{-2}$, $b=0,0562\, Lmol^{-1}$
Jawaban Soal Hukum Gas Van der Waals & Gas Graham
Gas klorin ($\mbox{Cl}_{2}$) memiliki jumlah mol :
$71g\times\frac{1mol}{71g}=1mol$
kita ubah bentuk persamaan van der Waals untuk tekanan:
$\begin{aligned}P & =\frac{nRT}{V-nb}-\frac{n^{2}a}{V^{2}}\\
& =\frac{1\times0,082\times273}{2-1\times0,0562}-\frac{1^{2}\times6,49}{2^{2}}atm\\
& =9,9atm
\end{aligned}
$
Latihan Soal Hukum Gas Van der Waals & Gas Graham (Mudah)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Suatu gas akan cenderung bersifat non-ideal pada….
BetulSuatu gas akan cenderung bersifat non-ideal pada suhu rendah dan tekanan tinggi
SalahSuatu gas akan cenderung bersifat non-ideal pada suhu rendah dan tekanan tinggi
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Dalam sebuah percobaan gas helium (He) dan etilena ($\mbox{C}_{2}\mbox{H}_{4}$)diletakkan dalam dua wadah yang berbeda. Di dalam masing-masing wadah diberikan sekat dengan lubang yang sangat kecil, dimana masing-masing gas ditempatkan di salah satu sisi dan sisi lainnya dengan dibatasi sekat tadi divakumkan. Setelah beberapa saat, gas manakah yang terdistribusi lebih merata?
BetulMassa molekul masing-masing :
He : 4
Etilena : 14
Sehingga laju efusi helium akan lebih cepat dan distribusi molekul akan lebih merataSalahMassa molekul masing-masing :
He : 4
Etilena : 14
Sehingga laju efusi helium akan lebih cepat dan distribusi molekul akan lebih merata -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Apabila diketahui untuk gas klorin, konstanta van der Waalsnya adalah: $a=6,49\mbox{ L}^{2}\mbox{atm}.\mbox{mo}\mbox{l}^{-2}$ dan $b=0,0562\mbox{ L.mo}\mbox{l}^{-1}$, berapakah tekanan dari 1 mol gas klorin di dalam wadah berukuran 2 L dan suhu $27^{\circ}\mbox{C}$?
BetulUntuk gas non-ideal, kita gunakan persamaan:
$\begin{alignedat}{1}P & =\frac{nRT}{V-nb}-\frac{n^{2}a}{V^{2}}\\
& =\frac{1\times0,082\times300}{2-(1\times0,0562)}-\frac{1^{2}\times6,49}{2^{2}}\\
& =11,03\mbox{ atm.}
\end{alignedat}
$SalahUntuk gas non-ideal, kita gunakan persamaan:
$\begin{alignedat}{1}P & =\frac{nRT}{V-nb}-\frac{n^{2}a}{V^{2}}\\
& =\frac{1\times0,082\times300}{2-(1\times0,0562)}-\frac{1^{2}\times6,49}{2^{2}}\\
& =11,03\mbox{ atm.}
\end{alignedat}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Bila $2,2\times10^{-4}$mol gas $\mbox{N}_{2}$ mengalami efusi melalui suatu lubang kecil selama 105 detik, berapa banyak gas hidrogen yang akan melewati lubang yang sama dalam waktu yang sama?
BetulSesuai Hukum Graham:
$\begin{aligned}\frac{\mbox{mol H}_{2}}{2,2\times10^{-4}\mbox{mol N}_{2}} & =\sqrt{\frac{Mr_{N_{2}}}{Mr_{H_{2}}}}\\
& =\sqrt{14}\\
\mbox{mol H}_{2} & =8,23\times10^{-4}
\end{aligned}
$SalahSesuai Hukum Graham:
$\begin{aligned}\frac{\mbox{mol H}_{2}}{2,2\times10^{-4}\mbox{mol N}_{2}} & =\sqrt{\frac{Mr_{N_{2}}}{Mr_{H_{2}}}}\\
& =\sqrt{14}\\
\mbox{mol H}_{2} & =8,23\times10^{-4}
\end{aligned}
$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
Berikut ini keterbatasan Hukum Graham adalah …
BetulHukum Graham hanya berlaku untuk efusi pada tekanan rendah, sehingga molekul gas yang teramati melewati lubang kecil secara individual atau satu per satu, bukan dalam jumlah besar.
SalahHukum Graham hanya berlaku untuk efusi pada tekanan rendah, sehingga molekul gas yang teramati melewati lubang kecil secara individual atau satu per satu, bukan dalam jumlah besar.
Latihan Soal Hukum Gas Van der Waals & Gas Graham (Sedang)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Jika 0,00484 mol gas dinitrogen monoksida mengalami efusi melalui suatu lubang pada periode waktu tertentu, berapa banyak gas nitrogen dioksida yang akan berefusi pada kondisi dan periode waktu yang sama?
BetulLaju efusi berbanding lurus dengan laju pergerakan molekul gas, maka dengan membandingkan $\mu_{\mbox{rms}}$ kedua zat, maka didapatkan hubungan untuk laju efusinya (hukum Graham):
$\begin{alignedat}{1}\frac{\mu_{\mbox{rms}}\mbox{N}_{2}\mbox{O}}{\mu_{\mbox{rms}}\mbox{N}\mbox{O}_{2}} & =\sqrt[2]{\frac{M_{\mbox{N}_{2}\mbox{O}}}{M_{\mbox{N}\mbox{O}_{2}}}}\\
& =\sqrt[2]{\frac{44}{46}}\\
& =0,978
\end{alignedat}
$Maka, jumlah $\mbox{N}\mbox{O}_{2}$ yang berefusi:
$\frac{1}{0,978}\times0,00484\,\mbox{mol}=0,00495\mbox{ mol.}$SalahLaju efusi berbanding lurus dengan laju pergerakan molekul gas, maka dengan membandingkan $\mu_{\mbox{rms}}$ kedua zat, maka didapatkan hubungan untuk laju efusinya (hukum Graham):
$\begin{alignedat}{1}\frac{\mu_{\mbox{rms}}\mbox{N}_{2}\mbox{O}}{\mu_{\mbox{rms}}\mbox{N}\mbox{O}_{2}} & =\sqrt[2]{\frac{M_{\mbox{N}_{2}\mbox{O}}}{M_{\mbox{N}\mbox{O}_{2}}}}\\
& =\sqrt[2]{\frac{44}{46}}\\
& =0,978
\end{alignedat}
$Maka, jumlah $\mbox{N}\mbox{O}_{2}$ yang berefusi:
$\frac{1}{0,978}\times0,00484\,\mbox{mol}=0,00495\mbox{ mol.}$ -
Pertanyaan ke 2 dari 5
2. Pertanyaan
Bila diketahui bahwa $2,2\times10^{-4}$mol gas $\mbox{N}_{2}$ mengalami efusi melalui suatu lubang kecil selama 105 detik, berapakah waktu yang diperlukan untuk gas $\mbox{H}_{2}$ dalam jumlah yang sama untuk mengalami efusi tersebut?
Betulkita gunakan Hukum Graham, karena waktu berbanding terbalik dengan laju, maka :
$\begin{aligned}\frac{t_{2}}{t_{1}} & =\sqrt{\frac{M_{2}}{M_{1}}}\\
\frac{t_{2}}{105\mbox{ s}} & =\sqrt{\frac{2}{28}}\\
t_{2} & =28,06\mbox{ s}
\end{aligned}
$Salahkita gunakan Hukum Graham, karena waktu berbanding terbalik dengan laju, maka :
$\begin{aligned}\frac{t_{2}}{t_{1}} & =\sqrt{\frac{M_{2}}{M_{1}}}\\
\frac{t_{2}}{105\mbox{ s}} & =\sqrt{\frac{2}{28}}\\
t_{2} & =28,06\mbox{ s}
\end{aligned}
$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Pada persamaan van der Waals, konstanta b menunjukkan …
BetulPada persamaan van der Waals konstanta a menunjukkan konstanta proporsionalitas sementara konstanta b menunjukkan pengaruh dari volume molekul gas itu sendiri
SalahPada persamaan van der Waals konstanta a menunjukkan konstanta proporsionalitas sementara konstanta b menunjukkan pengaruh dari volume molekul gas itu sendiri
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Manakah di antara gas berikut yang akan memiliki nilai konstanta a paling tinggi?
BetulNilai konstanta a menunjukkan kuatnya interaksi intermolekuler pada molekul gas, yakni gaya van der Waals. Maka untuk mudahnya kita bandingkan massa molekul masing-masing gas, dimana yang paling besar tentu mempunyai interaksi intermolekul paling besar
- $\mbox{N}_{2}=28$
- $\mbox{CO}_{2}=44$
- $\mbox{CCl}_{4}=154$
- $\mbox{Cl}_{2}=71$
- $\mbox{H}_{2}\mbox{O}=18$
Maka, diperkirakan bahwa $\mbox{CCl}_{4}$ akan memiliki konstanta a paling tinggi.
SalahNilai konstanta a menunjukkan kuatnya interaksi intermolekuler pada molekul gas, yakni gaya van der Waals. Maka untuk mudahnya kita bandingkan massa molekul masing-masing gas, dimana yang paling besar tentu mempunyai interaksi intermolekul paling besar
- $\mbox{N}_{2}=28$
- $\mbox{CO}_{2}=44$
- $\mbox{CCl}_{4}=154$
- $\mbox{Cl}_{2}=71$
- $\mbox{H}_{2}\mbox{O}=18$
Maka, diperkirakan bahwa $\mbox{CCl}_{4}$ akan memiliki konstanta a paling tinggi.
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Dalam suatu percobaan, gas $\mbox{CO}_{2}$ sebanyak 1 mol ditempatkan di dalam wadah dengan volume 2L pada suhu 273 K. Bila diketahui bahwa konstanta van der Waalsnya adalah $a=3,66\mbox{ L}^{2}\mbox{atm mol}^{-2}$ dan $b=0,0427\mbox{ L.mol}^{-1}$ tentukan berapa persen penyimpangan tekanannya dari gas ideal?
BetulSesuai persamaan gas ideal :
$\begin{aligned}PV & =nRT\\
P\times2 & =1\times0,082\times273\mbox{ atm}\\
P & =11,193\mbox{ atm}
\end{aligned}
$Sementara, untuk persamaan non-ideal:
$\begin{alignedat}{1}P & =\frac{nRT}{V-nb}-\frac{n^{2}a}{V^{2}}\\
& =\frac{1\times0,082\times273}{2-(1\times0,0427)}-\frac{1^{2}\times3,66}{2^{2}}\\
& =10,522\mbox{ atm.}
\end{alignedat}
$Maka, besar penyimpangannya adalah
$\frac{11,193-10,522}{11,193}\times100%=6%$SalahSesuai persamaan gas ideal :
$\begin{aligned}PV & =nRT\\
P\times2 & =1\times0,082\times273\mbox{ atm}\\
P & =11,193\mbox{ atm}
\end{aligned}
$Sementara, untuk persamaan non-ideal:
$\begin{alignedat}{1}P & =\frac{nRT}{V-nb}-\frac{n^{2}a}{V^{2}}\\
& =\frac{1\times0,082\times273}{2-(1\times0,0427)}-\frac{1^{2}\times3,66}{2^{2}}\\
& =10,522\mbox{ atm.}
\end{alignedat}
$Maka, besar penyimpangannya adalah
$\frac{11,193-10,522}{11,193}\times100%=6%$
Latihan Soal Hukum Gas Van der Waals & Gas Graham (Sukar)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Arsen (III) sulfida diketahui mudah menyublim, dan partikel uapnya diketahui dapat berefusi 0,28 kali lebih cepat dibanding Ar pada kondisi yang sama. Manakah rumus molekul yang tepat untuk arsen (III) sulfida ini pada fase gas?
BetulKita gunakan hukum Graham untuk menghitung massa molekul (MM) arsen (III) sulfida:
$\frac{\mbox{laju sulfida}}{\mbox{laju Ar}}=\left[\frac{39,9}{MM(\mbox{sulfida})}\right]^{1/2}=0,28$Maka,
$MM\mbox{ sulfida}=\frac{39,9}{0,28^{2}}=509\mbox{ g/mol.}$Rumus empiris arsen (III) sulfida adalah $\mbox{A}\mbox{s}_{2}\mbox{S}_{3}$, dengan massa formula 246 sehingga:
$\begin{alignedat}{1}246,1\times n & =509\\
& \approx2
\end{alignedat}
$Sehingga rumus molekulnya pada fase gas adalah $\mbox{A}\mbox{s}_{4}\mbox{S}_{6}$.
SalahKita gunakan hukum Graham untuk menghitung massa molekul (MM) arsen (III) sulfida:
$\frac{\mbox{laju sulfida}}{\mbox{laju Ar}}=\left[\frac{39,9}{MM(\mbox{sulfida})}\right]^{1/2}=0,28$Maka,
$MM\mbox{ sulfida}=\frac{39,9}{0,28^{2}}=509\mbox{ g/mol.}$Rumus empiris arsen (III) sulfida adalah $\mbox{A}\mbox{s}_{2}\mbox{S}_{3}$, dengan massa formula 246 sehingga:
$\begin{alignedat}{1}246,1\times n & =509\\
& \approx2
\end{alignedat}
$Sehingga rumus molekulnya pada fase gas adalah $\mbox{A}\mbox{s}_{4}\mbox{S}_{6}$.
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Menurut data pada suatu buku, gas $\mbox{O}_{2}$ memiliki volume molar sebesar 0,2168 $\mbox{L.mol}^{-1}$ pada 280 K dan 10 MPa. Gunakan persamaan gas non-ideal untuk menghitung nilai tekanan yang seharusnya dilepaskan gas $\mbox{O}_{2}$ tersebut! Berapa besar penyimpangannya dari data pada buku tersebut? ($a=1,382\mbox{ L}^{2}\mbox{atm.mol}^{-2}$ dan $b=0,0319\mbox{ L.mol}^{-1}$ )
Betul$\begin{alignedat}{1}P & =\frac{nRT}{V-nb}-\frac{n^{2}a}{V^{2}}\\
& =\frac{1\times0,082\times280}{0,2168-(1\times0,0319)}-\frac{1^{2}\times1,382}{0,2168^{2}}\\
& =94,771\mbox{ atm.}
\end{alignedat}
$Bila dikonversikan ke pascal :
$\frac{101325\mbox{ Pa}}{1\mbox{ atm}}\times94,771\mbox{ atm}=9,6\mbox{ MPa}$Sehingga, besar penyimpangannya dari data adalah :
$\frac{10-9,6}{10}\times100\%=4%$Salah$\begin{alignedat}{1}P & =\frac{nRT}{V-nb}-\frac{n^{2}a}{V^{2}}\\
& =\frac{1\times0,082\times280}{0,2168-(1\times0,0319)}-\frac{1^{2}\times1,382}{0,2168^{2}}\\
& =94,771\mbox{ atm.}
\end{alignedat}
$Bila dikonversikan ke pascal :
$\frac{101325\mbox{ Pa}}{1\mbox{ atm}}\times94,771\mbox{ atm}=9,6\mbox{ MPa}$Sehingga, besar penyimpangannya dari data adalah :
$\frac{10-9,6}{10}\times100\%=4%$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Seorang ilmuwan Amerika melakukan percobaan berikut. Dua buah gas dengan jumlah masing-masing 2 mol diletakkan dalam suatu kondisi eksperimen yang serupa, di dalam wadah 1 L dan suhu 80,33 Fahrenheit. Kedua gas tesebut adalah karbon dioksida ($a=3,66\mbox{ L}^{2}\mbox{atm mol}^{-2}$ dan $b=0,0427\mbox{ L mol}^{-1}$) dan karbon monoksida ($a=1,47\mbox{ L}^{2}\mbox{atm mol}^{-2}$ dan $b=0,0395\mbox{ L mol}^{-1})$. Manakah diantara kedua gas ini yang menunjukkan penyimpangan lebih besar dari gas idealnya, dan berapakah selisih persentase penyimpangan keduanya?
BetulPertama kita konversi Fahrenheit (sistem Imperial yang masih digunakan di AS) ke Kelvin.
$\begin{aligned}T_{(K)} & =\left(T_{(F)}+459,67\right)\times\frac{5}{9}\\
& =(80,33+459,67)\times\frac{5}{9}\\
& =300\mbox{ K}
\end{aligned}
$Maka, kita hitung nilai tekanan gas keduanya dalam kondisi ideal:
$\begin{aligned}PV & =nRT\\
P\times1 & =2\times0,082\times300\\
P & =49,2\mbox{ atm}
\end{aligned}
$Kemudian dalam kondisi nyata:
Untuk :$\mbox{CO}_{2}$
$\begin{alignedat}{1}P & =\frac{nRT}{V-nb}-\frac{n^{2}a}{V^{2}}\\
& =\frac{2\times0,082\times300}{1-(2\times0,0427)}-\frac{2^{2}\times3,66}{1^{2}}\\
& =39,154\mbox{ atm.}
\end{alignedat}
$Besar penyimpangannya:
$\frac{49,2-39,154}{49,2}\times100%=20,418%$Untuk CO :
$\begin{alignedat}{1}P & =\frac{nRT}{V-nb}-\frac{n^{2}a}{V^{2}}\\
& =\frac{2\times0,082\times300}{1-(2\times0,0395)}-\frac{2^{2}\times1,47}{1^{2}}\\
& =47,54\mbox{ atm.}
\end{alignedat}
$Besar penyimpangannya
$\frac{49,2-47,54}{49,2}\times100\%=3,374\%$Sehingga $\mbox{CO}_{2}$ memiliki penyimpangan lebih besar dengan
selisih :
$20,418%-3,374%=17,044%$SalahPertama kita konversi Fahrenheit (sistem Imperial yang masih digunakan di AS) ke Kelvin.
$\begin{aligned}T_{(K)} & =\left(T_{(F)}+459,67\right)\times\frac{5}{9}\\
& =(80,33+459,67)\times\frac{5}{9}\\
& =300\mbox{ K}
\end{aligned}
$Maka, kita hitung nilai tekanan gas keduanya dalam kondisi ideal:
$\begin{aligned}PV & =nRT\\
P\times1 & =2\times0,082\times300\\
P & =49,2\mbox{ atm}
\end{aligned}
$Kemudian dalam kondisi nyata:
Untuk :$\mbox{CO}_{2}$
$\begin{alignedat}{1}P & =\frac{nRT}{V-nb}-\frac{n^{2}a}{V^{2}}\\
& =\frac{2\times0,082\times300}{1-(2\times0,0427)}-\frac{2^{2}\times3,66}{1^{2}}\\
& =39,154\mbox{ atm.}
\end{alignedat}
$Besar penyimpangannya:
$\frac{49,2-39,154}{49,2}\times100%=20,418%$Untuk CO :
$\begin{alignedat}{1}P & =\frac{nRT}{V-nb}-\frac{n^{2}a}{V^{2}}\\
& =\frac{2\times0,082\times300}{1-(2\times0,0395)}-\frac{2^{2}\times1,47}{1^{2}}\\
& =47,54\mbox{ atm.}
\end{alignedat}
$Besar penyimpangannya
$\frac{49,2-47,54}{49,2}\times100\%=3,374\%$Sehingga $\mbox{CO}_{2}$ memiliki penyimpangan lebih besar dengan
selisih :
$20,418%-3,374%=17,044%$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Suatu molekul gas nitrogen dengan energi kinetik rata-rata pada suhu 300 K dilepaskan dari permukaan Bumi dan mengalami difusi ke atas. Bila diasumsikan bahwa molekul nitrogen berdifusi tanpa bertumbukan dengan molekul lainnya, berapa ketinggian maksimum yang dapat dicapai molekul tersebut? $\left(g=9,81\mbox{m.s}^{-2},\mbox{1 sma}=1,66\times10^{-27}\mbox{kg}\right)$
BetulPada titik maksimum, seluruh energi kinetik molekul gas dikonversikan ke energi potensial.
Maka, kita hitung energi kinetik rata-rata molekul gas:
$\begin{aligned}E_{k} & =\frac{3}{2}kT\\
& =\frac{3}{2}\times1,38\times10^{-23}\times300\\
& =6,21\times10^{-21}\mbox{J}
\end{aligned}
$untuk menghitung ketinggiannya, maka kita hitung massa 1 molekul nitrogen dalam kg :
$\frac{1,66\times10^{-27}\mbox{kg}}{1\mbox{ sma}}\times28\mbox{ sma}=4,648\times10^{-26}\mbox{kg}$Maka, dalam titik maksimum :
$\begin{aligned}Ek & =Ep\\
6,21\times10^{-21} & =mgh\\
6,21\times10^{-21} & =4,648\times10^{-26}\times9,81\times h\\
h & =13600\mbox{ m}\\
& =13,6\mbox{ km}
\end{aligned}
$SalahPada titik maksimum, seluruh energi kinetik molekul gas dikonversikan ke energi potensial.
Maka, kita hitung energi kinetik rata-rata molekul gas:
$\begin{aligned}E_{k} & =\frac{3}{2}kT\\
& =\frac{3}{2}\times1,38\times10^{-23}\times300\\
& =6,21\times10^{-21}\mbox{J}
\end{aligned}
$untuk menghitung ketinggiannya, maka kita hitung massa 1 molekul nitrogen dalam kg :
$\frac{1,66\times10^{-27}\mbox{kg}}{1\mbox{ sma}}\times28\mbox{ sma}=4,648\times10^{-26}\mbox{kg}$Maka, dalam titik maksimum :
$\begin{aligned}Ek & =Ep\\
6,21\times10^{-21} & =mgh\\
6,21\times10^{-21} & =4,648\times10^{-26}\times9,81\times h\\
h & =13600\mbox{ m}\\
& =13,6\mbox{ km}
\end{aligned}
$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
Diketahui massa jenis nyata dari gas-gas berikut pada suhu $20,0^{\circ}C$ dan tekanan 1 atm : $\mbox{O}_{2}=1,331$ g/L, $\mbox{OF}_{2}=2,26$ g/L dan NO$=1,249$ g/L. Urutkanlah dari yang paling sesuai dengan gas ideal hingga yang paling tidak sesuai.
BetulKita hitung densitas masing-masing berdasarkan hukum gas ideal
$\rho=\frac{Mr\times P}{RT}$untuk masing-masing gas:
- $\mbox{O}_{2}$
$\begin{aligned}\rho & =\frac{Mr\times P}{RT}\\
& =\frac{32\times1}{0,082\times293}\\
& =1,3319
\end{aligned}
$Besar penyimpangannya:$\frac{1,3319-1,331}{1,3319}\times100%=0,0675%$
- $\mbox{OF}_{2}$
$\begin{aligned}\rho & =\frac{Mr\times P}{RT}\\
& =\frac{54\times1}{0,082\times293}\\
& =2,2475
\end{aligned}
$Besar penyimpangannya
$\frac{2,26-2,2475}{2,2475}\times100%=0,556%$ - NO
$\begin{aligned}\rho & =\frac{Mr\times P}{RT}\\
& =\frac{30\times1}{0,082\times293}\\
& =1,2486
\end{aligned}
$Besar penyimpangannya$\frac{1,249-1,2486}{1,2486}\times100\%=0,032\%$
Maka urutannya dari yang paling sesuai ke yang tidak sesuai dengan gas ideal: NO, $\mbox{O}_{2}$, $\mbox{OF}_{2}$
SalahKita hitung densitas masing-masing berdasarkan hukum gas ideal
$\rho=\frac{Mr\times P}{RT}$untuk masing-masing gas:
- $\mbox{O}_{2}$
$\begin{aligned}\rho & =\frac{Mr\times P}{RT}\\
& =\frac{32\times1}{0,082\times293}\\
& =1,3319
\end{aligned}
$Besar penyimpangannya:$\frac{1,3319-1,331}{1,3319}\times100%=0,0675%$
- $\mbox{OF}_{2}$
$\begin{aligned}\rho & =\frac{Mr\times P}{RT}\\
& =\frac{54\times1}{0,082\times293}\\
& =2,2475
\end{aligned}
$Besar penyimpangannya
$\frac{2,26-2,2475}{2,2475}\times100%=0,556%$ - NO
$\begin{aligned}\rho & =\frac{Mr\times P}{RT}\\
& =\frac{30\times1}{0,082\times293}\\
& =1,2486
\end{aligned}
$Besar penyimpangannya$\frac{1,249-1,2486}{1,2486}\times100\%=0,032\%$
Maka urutannya dari yang paling sesuai ke yang tidak sesuai dengan gas ideal: NO, $\mbox{O}_{2}$, $\mbox{OF}_{2}$
