Ingin mempelajari materi kimia, khususnya tentang Entropi & Energi Bebas Gibbs? Supaya lebih paham, kamu bisa menyimak pembelajarannya di sini. Kamu juga bisa mengerjakan soal latihan untuk mempraktikkan materi yang telah dijelaskan.
Lewat pembahasan ini, kamu bisa belajar mengenai Entropi & Energi Bebas Gibbs. Kamu akan diajak untuk memahami materi dan tentang metode menyelesaikan soal.
Kamu juga akan memperoleh latihan soal interaktif yang tersedia dalam tiga tingkat kesulitan, yaitu mudah, sedang, dan sukar. Tertarik untuk mempelajarinya?
Sekarang, kamu bisa mulai mempelajari materi lewat uraian berikut. Apabila materi ini berguna, bagikan ke teman-teman kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & contoh soal serta kumpulan latihan soal Entropi & Energi Bebas Gibbs dalam bentuk pdf pada link dibawah ini:
Definisi
- Pengertian entropi (S) adalah ukuran keacakan atau ketidakteraturan suatu sistem
- Pengertian energi bebas gibbs adalah energi yang tersedia untuk melakukan kerja
Entropi
1. Entropi (S)
Entropi (S) adalah ukuran keacakan} atau ketidakteraturan suatu sistem. Berbeda dengan entalpi, entropi mutlak suatu zat dapat diketahui sebagai entropi standar yaitu entropi mutlak suatu zat pada 1 atm dan 25$^{0}C$ dengan satuan JK $^{-1}$atau JK$^{-1}$mol$^{-1}$ untuk satu mol zat. Entropi unsur dan senyawa semua bernilai positif ($S^{\circ}>0)$.
$\triangle S=S_{f}-S_{i}$
persamaan diatas menunjukan bahwa entropi merupakan suatu fungsi keadaandengan, dimana
$\begin{aligned}\triangle S & =\mbox{perubahan entropi}\\ S_{f} & =\mbox{entropi pada keadaan akhir }(final\, state)\\ S_{i} & =\mbox{entropi pada keadaan awal }(initial\, state) \end{aligned}$
2. Berdasarkan Hukum Kedua Termodinamika
“Entropi semesta meningkat dalam proses spontan dan tidak berubah pada proses kesetimbangan”
$\begin{aligned}\triangle S_{univ} & =\triangle S_{sis}+\triangle S_{surr}\,\,\,>\mbox{0 (spontan)}\\ \triangle S_{univ} & =\triangle S_{sis}+\triangle S_{surr}\,\,\,=\mbox{0 (kesetimbangan)} \end{aligned}$
dengan,
$\begin{aligned}\triangle S_{univ} & =\mbox{perubahan entropi semesta }(universe)\\ \triangle S_{sis} & =\mbox{perubahan entropi sistem }(system)\\ \triangle S_{surr} & =\mbox{perubahan entropi lingkungan}(surronding) \end{aligned}$.
3. Perubahan Entropi Sistem
Andaikan sistem dinyatakan dengan reaksi berikut
$a$A $+$$b$B $\rightarrow c\mbox{C }+d\mbox{D}$
sebagaimana halnya entalpi reaksi, \emph{entropi reaksi standar}$\triangle S_{rxn}^{\circ}$ adalah
$\triangle S_{rxn}^{\circ}=\Sigma nS^{\circ}(\mbox{produk)}+\Sigma nS^{\circ}(\mbox{reaktan)}$
4. Perubahan entropi dalam lingkungan
Bila suatu proses eksotermik berlangsung dalam suatu sistem, kalor yang dipindahkan ke lingkungan meningkatkan gerakan molekul di lingkungan.
Akibatya, ada peningkatan ketidakteratuan pada tingkat molekul, dan entropi lingkungan meningkat. Sebaliknya, proses endotermik dalam sistem menyerap kalor dari lingkungan dan dengan demikian menurunkan entropi lingkungan karena gerakan molekul berkurang.
Untuk proses pada tekanan, perubahan kalor sama dengan perubahan entalpi sistem, $\triangle H.$ dengan demikian perubahan entropi lingkungan $\triangle S$ akan berbanding lurus terhadapa $\triangle H$ sistem.
$\triangle S_{surr}\varpropto-\triangle H_{sis}$ untuk proses eksotemik
$-\triangle S_{surr}\varpropto+\triangle H_{sis}$ untuk proses endotemik
Perubahan entropi untuk sejumlah tertentu kalor juga bergantung pada suhu. Semakin tinggi suhu semakin kecil $\triangle S_{surr}$ dan semakin rendah suhu semakin besar $\triangle S_{surr}$
$\triangle S_{surr}=\frac{-\triangle H}{T}$
Energi Bebas Gibbs
1. Kespontanan Reaksi
Kespontanan reaksi dapat juga dinyatakan dalam energi bebas Gibbs (G), atau energi bebas.
$G=H-TS$
karena energi bebas merupakan fungsi keadaan maka persaam diatas menjadi (pada suhu tetap)
$\triangle G=\triangle H-T\triangle S$
ketika :
$\begin{aligned}\triangle G & <\mbox{0 Reaksi spontan ke arah kedepan}\\ \triangle G & >\mbox{0 Reaksi nonspontan. Reaksi ini spontan pada arah yang berlawanan}\\ \triangle G & =0\mbox{ Sistem bereda pada kesetimbangan} \end{aligned} $
2. Hubungan $\triangle H$ dan $\triangle S$ untuk memprediksi kespontanan suatu reaksi
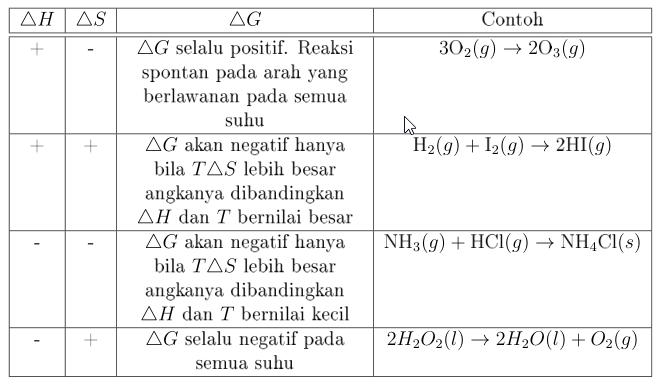
3. Perubahan Energi Bebas Standar
Energi bebas reaksi standar ($\triangle G_{rxn}^{\circ}$) ialah perubahan energi-bebas untuk reaksi bila reaksi itu terjadi pada kondisi keadaan standar, artinya, bila reaktan berada dalam keadaan standarnya diubah menjadi produk dalam keadaan standarnya. Untuk menghitung $\triangle G_{rxn}^{\circ}$ maka perlu dilihat persamaan reaksinya
$aA+bB\rightarrow cC+dD$
Perubahab $\triangle G_{rxn}^{\circ}$ untuk reaksi ini ialah
$\triangle G_{rxn}^{\circ}=[(c\triangle G_{f}^{\circ}C+d\triangle G_{f}^{\circ}D)-(a\triangle G_{f}^{\circ}A+b\triangle G_{f}^{\circ}B)]$
atau
$\triangle G_{rxn}^{\circ}=\Sigma nG^{\circ}(\mbox{produk)}+\Sigma nG^{\circ}(\mbox{reaktan)}$
4. Energi bebas dan Kesetimbangan
Tidak mudah mempertahankan sistem kesetimbangan pada keadaan standar. Banyak reaksi-reaksi tidak berada pada keadaan standar, maka untuk keadaan yang demikian arah reaksi tidak dapat diprediksi hanya dengan nilai$\triangle G^{\circ}$, melainkan harus menggakan energi bebas actual $\triangle G$. Hubungan $\triangle G$ dan $\triangle G^{\circ}$ yang diturunkan dari termodinamika ialah
$\triangle G=\triangle G^{\circ}+RT\, ln\, Q$
dimana
$\triangle G^{\circ}$ tetap pada suhu tertentu $\begin{aligned}T & =\mbox{suhu mutlak reaksi}\\ R & =\mbox{konstanta gas (8,314 J/K)}\\ Q & =\mbox{kuosien reaksi} \end{aligned}$
Pada kesetimbangan, berdasarkan definisi, $\triangle G=0$ dan $Q=K$, dimana $K$ adalah konstanta kesetimbangan, maka
$\begin{aligned}\triangle G & =\triangle G^{\circ}+RT\, ln\, Q\\ & =\triangle G^{\circ}+RT\, ln\, Q\\ \triangle G^{\circ} & =-RT\, ln\, Q \end{aligned} $
Dalam persamaan ini $K_{p}$ digunakan untuk gas dan $K_{c}$ untuk reaksi dalam larutan.
Contoh Soal Entropi & Energi Bebas Gibbs Beserta Pembahasannya
1. Kalor lebur molar dan kalor penguapan molar benzena masing-masing $10.9\, kJ/mol$ dan $31.0\, kJ/mol$ . Hitung perubahan entropi untuk transisi padatan $\rightarrow$ cairan dan cairan $\rightarrow$ uap untuk benzena. Pada tekanan 1 atm, benzena meleleh pada $5.5^{\circ}C$ dan mendidih pada $80.1^{\circ}C.$
Jawaban
(a) $\triangle S_{fus}$
$\begin{aligned}\triangle G & =\triangle H-T\triangle S\end{aligned}$
karena pada titik leleh, padatan benzena dan cairan benzena berada pada kesetimbangan. Jadi, $\triangle G=0$
$\begin{aligned}\triangle G & =\triangle H-T\triangle S\\ & =\triangle H-T\triangle S\\ \triangle S & =\frac{\triangle H_{fuss}}{T_{f}}\\ & =\frac{(10.9\, kJ/mol)(1000\, J/kJ)}{(5,5+273)K}\\ & =39.1\, J/K.mol \end{aligned} $
(b) $\triangle S_{vap}$
demikian pula, pada titik didih $\triangle G=0$ dan kita dapatkan
$\triangle S=\frac{\triangle H_{vap}}{T_{bp}}=\frac{(31.0\, kJ/mol)(1000\, J/kJ)}{(801+273)K}=87.8\, J/K.mol$
2. Pada industri ammonia sejumlah gas nitrogen direaksikan dengan gas hidrogen agar membentuk gas ammonia. Reaksi yang terjadi adalah sebagai berikut
$\mbox{N}_{2}(g)+3\mbox{H}_{2}(g)\rightleftharpoons2\mbox{NH}{}_{3}(g)$
jika diketahui perubahan energi bebas standar dari reaksi tersebut sebesar $-33.2\, kJ$ dan konstanta kesetimbangan, $K_{p}$ ialah $6.5\times10^{5}$ pada $25^{\circ}C$. Dalam suatu percobaan, tekanan awal adalah $P_{H_{2}}=\mbox{0.250 atm,}P_{N_{2}}=\mbox{0.870 atm dan}P_{NH_{3}}=12.9\mbox{ atm}$. Tentukan $\triangle G$ dan prediksi arah reaksi!
Jawaban
$\begin{aligned}\triangle G & =\triangle G^{\circ}+\mbox{RT lnQ}\\ & \triangle G^{\circ}+\mbox{RT\,\ ln}\frac{P_{NH_{3}}^{2}}{(P_{H_{2}}^{2})(P_{N_{2}})}\\ & =-33.2\times1000\, J/mol+(8.314\, J/K)(298\, K)\times ln\frac{(12.9)^{2}}{(0.250)^{3}(0.870)}\\ & =-33.2\times10^{3}\, J/mol+23,3\times10^{3}J/mol\\ & =-9.9\times10^{3}J/mol=-9.9\, kJ/mol \end{aligned}$.
