Ingin mempelajari Orde Reaksi & Waktu Paruh secara lebih mendalam? Kamu bisa menyimak baik-baik pembahasan berikut. Setelahnya, kamu bisa mengerjakan kuis berupa latihan soal untuk mengasah kemampuan.
Lewat pembahasan ini, kamu bisa belajar mengenai Orde Reaksi & Waktu Paruh. Kamu akan diajak untuk memahami materi dan tentang metode menyelesaikan soal.
Kamu juga akan memperoleh latihan soal interaktif yang tersedia dalam tiga tingkat kesulitan, yaitu mudah, sedang, dan sukar. Tertarik untuk mempelajarinya?
Sekarang, kamu bisa mulai mempelajari materi lewat uraian berikut. Apabila materi ini berguna, bagikan ke teman-teman kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & contoh soal serta kumpulan latihan soal Orde Reaksi & Waktu Paruh dalam bentuk pdf pada link dibawah ini:
Definisi
Pada halaman ini akan dibahas mengenai orde reaksi kimia & waktu paruh.
- Orde Reaksi adalah Pangkat konsentrasi pereaksi pada persamaan laju reaksi
- Waktu Paruh adalah Waktu yang dibutuhkan untuk sejumlah zat agar berkurang menjadi setengah dari nilai atau jumlah awalnya.
Orde Reaksi
Pada reaksi:
$\mbox{A}+\mbox{B}\rightarrow\mbox{C}+\mbox{D}$
dengan persamaan laju
$v=k[\mbox{A}]^{x}[\mbox{B}]^{y}$
$x$ dan $y$ adalah orde, atau pangkat konsentrasi pereaksi masing-masing (A dan B) terhadap persamaan laju reaksi. Sementara yang disebut orde reaksi adalah keseluruhan atau penjumlahan orde-orde setiap pereaksi, dalam contoh di atas berarti nilainya adalah $x+y$.
Orde reaksi biasanya adalah suatu bilangan bulat positif sederhana, meskipun ada pula yang bernilai 0, $\frac{1}{2}$, atau bilangan negatif. Beberapa orde reaksi yang umum antara lain:
1. Orde Nol
Orde nol atau orde reaksi nol merupakan suatu reaksi dikatakan berorde nol terhadap salah satu pereaksinya apabila perubahan konsentrasi pereaksinya tidak memengaruhi laju reaksi.
Bila diplot konsentrasi suatu pereaksi (sumbu X) vs laju reaksi ($v$) maka akan didapat grafik :

2. Orde Satu
Orde reaksi 1 atau suatu reaksi orde satu terhadap salah satu pereaksinya jika laju reaksinya berbanding lurus dengan konsentrasi pereaksi itu.
Sebagai contoh bila konsentrasi pereaksi dilipat-duakan, maka laju reaksi akan menjadi $2^{1}=2$ kali lipatnya. Bila diplot akan terbentuk kurva berikut:

3. Orde Dua
Suatu reaksi disebut berorde dua terhadap salah satu pereaksi, jika laju reaksi merupakan pangkat dua dari konsentrasi pereaksi itu.
Sebagai contoh bila konsentrasi pereaksi dilipat-duakan, maka laju reaksi akan menjadi $2^{2}=4$ kali lipatnya. Bila diplot akan didapat kurva berikut:
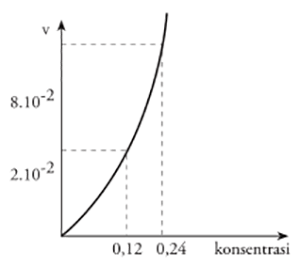
4. Orde Negatif
Suatu reaksi berorde negatif jika laju reaksi berbanding terbalik dengan konsentrasi pereaksi itu. Sebagai contoh bila suatu reaksi berorde -1, bila konsentrasi pereaksi dilipat-duakan, maka laju reaksi akan menjadi $2^{-1}=\frac{1}{2}$ kalinya.
Waktu Paruh
1. Orde nol
- Persamaan lajunya
$V=k[A]^{0}=k$ - Hubungan konsentrasi dengan waktu
$[A]_{0}-[A]_{t}=kt$”
dimana,
$[A]_{t}=$ konsentrasi pereaksi pada waktu $t$
$[A]_{0}=$ konsentrasi pereaksi awal
$k=$ konstanta laju reaksi
$t=$ waktu reaksi - Waktu paruh
Sehingga, untuk mengetahui waktu paruh (dilambangkan $t_{1/2}$), yakni waktu yang diperlukan ketika $[A]_{t}=\frac{1}{2}[A]_{0}$, kita masukkan ke persamaan di atas:
$\begin{alignedat}{1}[A]_{0}-[A]_{t} & =kt_{\frac{1}{2}}\\
{}[A]_{0}-\frac{1}{2}[A]_{0} & =kt_{\frac{1}{2}}\\
\frac{1}{2}[A]_{0} & =kt_{\frac{1}{2}}\\
t_{\frac{1}{2}} & =\frac{[A]_{0}}{2k}
\end{alignedat}
$
2. Orde satu
- Persamaan lajunya
$V=k[A]$ - Hubungan konsentrasi dengan waktu
$\ln\frac{[A]_{0}}{[A]_{t}}=kt$ atau $\ln\frac{[A]_{t}}{[A]_{0}}=-kt$ - Waktu paruh
$t_{\frac{1}{2}}=\frac{0,693}{k}$
Sehingga, untuk mengetahui waktu paruh (dilambangkan $t_{1/2}$), yakni waktu yang diperlukan ketika $[A]_{t}=\frac{1}{2}[A]_{0}$, kita masukkan ke persamaan di atas:$\begin{aligned}\ln\frac{\frac{1}{2}[A]_{0}}{[A]_{0}} & =-k\times t_{1/2}\\
t_{1/2} & =\frac{\ln2}{k}\\
& =\frac{0,693}{k}
\end{aligned}
$
3. Orde dua
- Persamaan lajunya
$V=k[A]^{2}$ - Hubungan konsentrasi dengan waktu
$\frac{1}{[A]_{t}}-\frac{1}{[A]_{0}}=kt$ - Waktu paruh
$t_{\frac{1}{2}}=\frac{1}{k[A]_{0}}$
Contoh Soal Orde Reaksi & Waktu Paruh dan Pembahasannya
- Suatu reaksi berorde 3 terhadap salah satu pereaksinya. Tentukan besarnya laju reaksi bila:
(a) Konsentrasi pereaksi dilipat-duakan;
(b) Konsentrasi pereaksi diperkecil 3 kali
Jawaban- Bila konsentrasi dilipat-duakan, maka laju akan menjadi $2^{3}=8$ kali lipat lebih cepat
- Bila konsentrasi diperkecil tiga kali maka laju akan menjadi $\left(\frac{1}{3}\right)^{3}=\frac{1}{27}$ kali dari laju awalnya, atau 27 kali lebih lambat.
- Bila diketahui reaksi: $\mbox{N}_{2}+3\mbox{H}_{2}\rightarrow2\mbox{NH}_{3}$ memiliki persamaan laju $v=k[\mbox{N}_{2}][\mbox{H}_{2}]^{2}$, lengkapilah tabel berikut.

Jawaban- ada percobaan II, konsentrasi nitrogen tetap sementara hidrogen diperkecil 2 kali atau setengahnya, maka laju reaksi akan menjadi: $0,5^{2}=0,25$, sehingga laju menjadi $0,25y$
- Pada percobaan III, dibandingkan dengan percobaan II konsentrasi hidrogen tetap sementara konsentrasi nitrogen menjadi 2 kali lipat, sehingga laju reaksi akan menjadi $2^{1}\times0,25y=0,5y$
- Pada percobaan IV, dibandingkan percobaan I, konsentrasi nitrogen menjadi setengahnya sementara konsentrasi hidrogen adalah 1,5 kalinya, sehingga laju reaksi menjadi: $0,5^{1}\times1,5^{2}\times y=1,125y$
- Diketahui reaksi dekomposisi $\mbox{H}_{2}\mbox{O}_{2}$ menghasilkan air dan gas oksigen memiliki waktu paruh sebesar 990 detik. Tentukan jumlah $\mbox{H}_{2}\mbox{O}_{2}$ yang telah terdekomposisi pada detik ke-500!
Jawaban
Pertama-tama kita tentukan nilai konstanta laju:
$\begin{aligned}t_{1/2} & =\frac{0,693}{k}\\
k & =\frac{0,693}{990}\mbox{s}^{-1}\\
& =0,0007\mbox{s}^{-1}
\end{aligned}
$Maka, pada detik ke-500:
$\begin{aligned}\ln\frac{[A]_{t}}{[A]_{0}} & =-kt\\
\ln x & =-0,0007\times500\\
x & =0,7047
\end{aligned}
$ bila $\frac{[A]_{t}}{[A]_{0}}$ kita misalkan $x$Sehingga, fraksi $\mbox{H}_{2}\mbox{O}_{2}$ yang terdekomposisi:
$1-0,7047=0,2953$
atau 29,53\% yang telah terdekomposisi