Tertarik untuk mempelajari materi fisika, khususnya tentang Energi Potensial Pegas? Jika iya, kamu bisa menyimak pembahasan lengkapnya di sini. Kami juga telah menyiapkan soal yang bisa kamu kerjakan sebagai latihan.
Lewat pembahasan ini, kamu bisa belajar mengenai Energi Potensial Pegas. Kamu akan diajak untuk memahami materi dan tentang metode menyelesaikan soal.
Kamu juga akan memperoleh latihan soal interaktif yang tersedia dalam tiga tingkat kesulitan, yaitu mudah, sedang, dan sukar. Tertarik untuk mempelajarinya?
Sekarang, kamu bisa mulai mempelajari materi lewat uraian berikut. Apabila materi ini berguna, bagikan ke teman-teman kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & kumpulan soal dalam bentuk pdf pada link dibawah ini:
Pengertian Energi Potensial Pegas
Sejumlah energi tentu dibutuhkan untuk meregangkan atau menekan pegas. Energi yang dimiliki pegas saat kondisi teregang atau tertekan merupakan salah satu bentuk energi potensial.
Energi Potensial Pegas
Mari kita tinjau sebuah pegas dengan konstanta $k$ yang terletak di atas lantai licin. Pegas diberi gaya luar sebesar $F$ sehingga ujung pegas bergeser sejauh $x.$

Pada kondisi ini maka pegas memberikan gaya pulih sebesar $F=-kx.$ Usaha yang dilakukan pegas dapat dihitung dengan mengintegralkan gaya pulih terhadap $x.$
Jika pada kondisi awal ujung pegas berada pada $x=x_{i}$ dan setelah diberi gaya luar ujung pegas berada pada posisi $x=x_{f}$ maka usaha yang dilakukan oleh pegas adalah sebesar $W.$
\begin{eqnarray}
W & = & \intop_{x_{i}}^{x_{f}}-kx\, dx\nonumber \\
W & = & \left[-\frac{1}{2}kx^{2}\right]_{x_{i}}^{x_{f}}\nonumber \\
W & = & \frac{1}{2}kx_{i}^{2}-\frac{1}{2}kx_{f}^{2}\\
W & = & E_{pi}-E_{pf}
\end{eqnarray}
Karena gaya luar bekerja berlawanan arah dengan gaya pulih pegas maka, besar usaha $(W_{eks})$ oleh gaya luar adalah
\begin{eqnarray}
W_{eks} & = & E_{pf}-E_{pi}
\end{eqnarray}
Usaha merupakan perubahan energi potensial, sehingga energi potensial dari sebuah pegas yang meregang sebesar $x$ dari kondisi setimbangnya dapat dituliskan rumus energi potensial pegas sebagai berikut.
\begin{eqnarray}
E_{p} & = & \frac{1}{2}kx^{2}
\end{eqnarray}
Jika kemudian gaya luar dihilangkan dan pegas digunakan untuk melontarkan beban bermassa $m$ dan beban $m$ bergerak dengan kecepatan $v$ maka energi potensial pegas berubah menjadi energi kinetik.

Diasumsikan semua energi potensial berubah menjadi energi kinetik maka pada kondisi ini berlaku hukum kekekalan energi mekanik.
\begin{eqnarray}
\Delta E_{p} & +\Delta E_{k}= & 0
\end{eqnarray}
Contoh Soal Energi Potensial Pegas dan Penyelesaiannya
- Pegas dengan konstanta 400 N/m digunakan sebagai pelontar peluru bermassa 10 gram. Hitung kecepatan peluru saat terlontar jika pegas ditekan sejauh 10 cm!
Penyelesaian:
Energi yang digunakan seluruhnya untuk melontarkan peluru, adalah
$\begin{alignedat}{1}E_{p} & =E_{k}\\
\frac{1}{2}kx^{2} & =\frac{1}{2}mv^{2}\\
v & =\sqrt{\frac{kx^{2}}{m}}\\
v & =\sqrt{\frac{400\times10^{-2}}{10^{-2}}}\\
v & =20\mbox{ m/s}
\end{alignedat}
$
- Pegas dengan konstanta 24 N/m digunakan sebagai pelontar peluru mainan secara vertikal. Agar peluru bermassa 100 gram dapat mencapai ketinggian 3 meter, pegas harus dimampatkan sebesar….
Penyelesaian:
Energi yang digunakan seluruhnya untuk melontarkan peluru, adalah
$\begin{alignedat}{1}x & =\sqrt{\frac{2mgh}{k}}\\
& =\sqrt{\frac{2\times0,1\times10\times3}{24}}\\
& =0,5\mbox{ m}
\end{alignedat}
$
Latihan Soal Energi Potensial Pegas (Mudah)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Energi untuk meregangkan pegas ditentukan oleh… .
BetulEnergi potensial pegas dipengaruhi oleh bahan pegas yang mempengaruhi nilai $k$, gaya eksternal yang menentukan pertambahan panjang dan pertambahan panjang yang terjadi.
SalahEnergi potensial pegas dipengaruhi oleh bahan pegas yang mempengaruhi nilai $k$, gaya eksternal yang menentukan pertambahan panjang dan pertambahan panjang yang terjadi.
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Energi yang dibutuhkan untuk meregangkan pegas dengan konstanta 200 N/m dari 50 cm menjadi 60 cm adalah… .
Betul$\begin{alignedat}{1}E_{pegas} & =\frac{1}{2}k(\Delta x)^{2}\\
& =\frac{1}{2}\times200\times0,1^{2}\\
& =1\mbox{ J.}
\end{alignedat}
$Salah$\begin{alignedat}{1}E_{pegas} & =\frac{1}{2}k(\Delta x)^{2}\\
& =\frac{1}{2}\times200\times0,1^{2}\\
& =1\mbox{ J.}
\end{alignedat}
$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Sebuah pegas ditarik dengan gaya sebesar 120 N sehingga pegas bertambah panjang dari 30 cm menjadi 35 cm. Energi yang digunakan adalah… .
Betul$\begin{alignedat}{1}E_{pegas} & =\frac{1}{2}F\Delta x\\
& =\frac{1}{2}\times120\times0,05\\
& =3\mbox{ J}.
\end{alignedat}
$Salah$\begin{alignedat}{1}E_{pegas} & =\frac{1}{2}F\Delta x\\
& =\frac{1}{2}\times120\times0,05\\
& =3\mbox{ J}.
\end{alignedat}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Suatu pegas membutuhkan energi 18 J untuk meregangkan pegas sebesar 6 cm. Konstanta pegas tersebut adalah… .
Betul$\begin{alignedat}{1}E_{pegas} & =\frac{1}{2}k(\Delta x)^{2}\\
k & =\frac{2E}{\Delta x^{2}}\\
& =\frac{36}{0,06^{2}}\\
& =10000\mbox{ Nm}^{-1}.
\end{alignedat}
$Salah$\begin{alignedat}{1}E_{pegas} & =\frac{1}{2}k(\Delta x)^{2}\\
k & =\frac{2E}{\Delta x^{2}}\\
& =\frac{36}{0,06^{2}}\\
& =10000\mbox{ Nm}^{-1}.
\end{alignedat}
$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
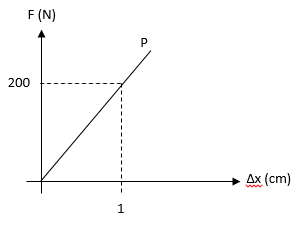
Grafik berikut menunjukkan hubungan antara gaya dengan pertambahan panjang pegas.

Energi potensial pegas saat pegas mengalami pertambahan panjang 10 cm adalah… .
BetulBerdasarkan grafik maka diperoleh konstanta pegasnya adalah $k=\frac{200}{0,01}=20000\mbox{ Nm}^{-1}$
sehingga energi potensia pegas saat bertambah panjang 10 cm adalah
$\begin{alignedat}{1}E_{pegas} & =\frac{1}{2}k(\Delta x)^{2}\\
& =\frac{1}{2}\times20000\times0,1^{2}\\
& =100\mbox{ J.}
\end{alignedat}
$SalahBerdasarkan grafik maka diperoleh konstanta pegasnya adalah $k=\frac{200}{0,01}=20000\mbox{ Nm}^{-1}$
sehingga energi potensia pegas saat bertambah panjang 10 cm adalah
$\begin{alignedat}{1}E_{pegas} & =\frac{1}{2}k(\Delta x)^{2}\\
& =\frac{1}{2}\times20000\times0,1^{2}\\
& =100\mbox{ J.}
\end{alignedat}
$
Latihan Soal Energi Potensial Pegas (Sedang)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Untuk meregangkan sebuah pegas sebesar 6 cm diperlukan energi sebesar 50 J. Energi yang dibutuhkan untuk meregangkan pegas sejauh 12 cm adalah… .
BetulEnergi potensial pegas sebanding dengan kuadrat regangannya, sehingga
$\begin{alignedat}{1}\frac{E_{1}}{E_{2}} & =\left(\frac{x_{1}}{x_{2}}\right)^{2}\\
E_{2} & =E_{1}\left(\frac{x_{2}}{x_{1}}\right)^{2}\\
& =50\left(\frac{12}{6}\right)^{2}\\
& =200\mbox{ J}.
\end{alignedat}
$SalahEnergi potensial pegas sebanding dengan kuadrat regangannya, sehingga
$\begin{alignedat}{1}\frac{E_{1}}{E_{2}} & =\left(\frac{x_{1}}{x_{2}}\right)^{2}\\
E_{2} & =E_{1}\left(\frac{x_{2}}{x_{1}}\right)^{2}\\
& =50\left(\frac{12}{6}\right)^{2}\\
& =200\mbox{ J}.
\end{alignedat}
$ -
Pertanyaan ke 2 dari 5
2. Pertanyaan
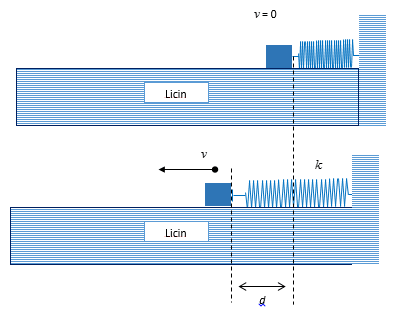
Balok ($m=1\mbox{ kg}$) digerakkan di atas lantai licin dengan kecepatan tetap sebesar $v=20$ m/s. Balok kemudian menghantam pegas mendatar sehingga pegas memendek 6 cm seperti gambar berikut dan balok berhenti kemudian bergerak berlawanan arah.

Konstanta pegas tersebut adalah… .
BetulKarena lintasan balok licin maka, energi kinetik balok berubah menjadi energi potensial pegas pada saat balok diam $(v=0)$. Secara matematis dituliskan sebagai:
$\begin{alignedat}{1}E_{pegas} & =E_{k\mbox{ balok}}\\
\frac{1}{2}kx^{2} & =\frac{1}{2}mv^{2}\\
k & =\frac{mv^{2}}{x^{2}}\\
& =\frac{1\times400}{36\times10^{-4}}\\
& =\frac{1}{9}\times10^{6}\mbox{Nm}^{-1}.
\end{alignedat}
$SalahKarena lintasan balok licin maka, energi kinetik balok berubah menjadi energi potensial pegas pada saat balok diam $(v=0)$. Secara matematis dituliskan sebagai:
$\begin{alignedat}{1}E_{pegas} & =E_{k\mbox{ balok}}\\
\frac{1}{2}kx^{2} & =\frac{1}{2}mv^{2}\\
k & =\frac{mv^{2}}{x^{2}}\\
& =\frac{1\times400}{36\times10^{-4}}\\
& =\frac{1}{9}\times10^{6}\mbox{Nm}^{-1}.
\end{alignedat}
$ -
Pertanyaan ke 3 dari 5
3. Pertanyaan
Pegas dengan kontanta pegas sebesar $k$ N/m bertambah panjang sebesar 8 cm saat digunakan untuk menggantung beban dengan massa 100 gram. Energi potensial pegas saat pegas ditarik dengan gaya sebesar 300 N adalah… .
Betul$\begin{alignedat}{1}k & =\frac{mg}{\Delta x}\\
& =\frac{1}{0,08}\\
& =12,5\mbox{ Nm}^{-1}
\end{alignedat}
$Jadi energi potensial pegasnya adalah $\frac{F^{2}}{2k}=\frac{300^{2}}{12,5}=7200\mbox{ J}.$
Salah$\begin{alignedat}{1}k & =\frac{mg}{\Delta x}\\
& =\frac{1}{0,08}\\
& =12,5\mbox{ Nm}^{-1}
\end{alignedat}
$Jadi energi potensial pegasnya adalah $\frac{F^{2}}{2k}=\frac{300^{2}}{12,5}=7200\mbox{ J}.$
-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Untuk meregangkan pegas dengan konstanta sebesar 200 N/m sepanjang $d$ cm dibutuhkan energi sebesar 1200 J. Energi yang dibutuhkan untuk meregangkan pegas Q yang memiliki konstanta sebesar 150 N/m sepanjang 2$d$ adalah… .
Betul$\begin{alignedat}{1}\frac{E_{1}}{E_{2}} & =\frac{200d^{2}}{150\times4d^{2}}\\
E_{2} & =3\times E_{1}\\
& =3\times1200\\
& =3600\mbox{ J}.
\end{alignedat}
$Salah$\begin{alignedat}{1}\frac{E_{1}}{E_{2}} & =\frac{200d^{2}}{150\times4d^{2}}\\
E_{2} & =3\times E_{1}\\
& =3\times1200\\
& =3600\mbox{ J}.
\end{alignedat}
$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
Pegas dengan konstanta 60 N/m digunakan sebagai pelontar peluru mainan secara vertikal. Agar peluru bermassa 100 gram dapat mencapai ketinggian 3 meter, pegas harus dimampatkan sebesar… .
BetulEnergi potensial pegas digunakan seluruhnya untuk melontarkan peluru, sehingga
$\begin{alignedat}{1}x & =\sqrt{\frac{2mgh}{k}}\\
& =\sqrt{\frac{2\times0,1\times10\times3}{60}}\\
& =0,32\mbox{ m}.
\end{alignedat}
$SalahEnergi potensial pegas digunakan seluruhnya untuk melontarkan peluru, sehingga
$\begin{alignedat}{1}x & =\sqrt{\frac{2mgh}{k}}\\
& =\sqrt{\frac{2\times0,1\times10\times3}{60}}\\
& =0,32\mbox{ m}.
\end{alignedat}
$
Latihan Soal Energi Potensial Pegas (Sukar)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Benda bermassa $m$ dilontarkan dengan pegas mendatar dari atas sebuah meja licin seperti gambar berikut.

Konstanta pegas $k$ dan pegas dimampatkan sebesar $d$. Kecepatan balok saat terlontar dari pegas adalah… .
BetulKarena lintasan balok licin maka, semua energi potensial pegas berubah menjadi energi kinetik balok. Secara matematis dituliskan sebagai:
$\begin{alignedat}{1}E_{pegas} & =E_{k\mbox{ balok}}\\
\frac{1}{2}kd^{2} & =\frac{1}{2}mv^{2}\\
v & =\sqrt{\frac{kd^{2}}{m}}.
\end{alignedat}
$SalahKarena lintasan balok licin maka, semua energi potensial pegas berubah menjadi energi kinetik balok. Secara matematis dituliskan sebagai:
$\begin{alignedat}{1}E_{pegas} & =E_{k\mbox{ balok}}\\
\frac{1}{2}kd^{2} & =\frac{1}{2}mv^{2}\\
v & =\sqrt{\frac{kd^{2}}{m}}.
\end{alignedat}
$ -
Pertanyaan ke 2 dari 5
2. Pertanyaan
Balok bermassa 1 kg dilontarkan dari bidang miring dengan menggunakan pegas dengan kontanta 400 N/m. Pegas dimampatkan sebesar 5 cm kemudian dilepaskan (perhatikan gambar) sehingga balok tepat terlempar dari puncak bidang miring. Jika kemiringan bidang $\alpha=37^{o}$ , ketinggian maksimum balok dihitung dari tanah adalah…. .
 Betul
BetulKecepatan balok di puncak bidang miring adalah
$\begin{alignedat}{1}v_{0} & =\sqrt{\frac{kd^{2}}{m}}\\
& =\sqrt{\frac{400\times0,05^{2}}{1}}\\
& =1\mbox{ ms}^{-1}
\end{alignedat}
$Kecepatan balok pada komponen vertikal adalah $v_{y}=v_{0}\mbox{sin 37}=0,6\mbox{ ms}^{-1}$
Ketinggian maskimum balok akibat komonen kecepatan ini adalah
$\begin{alignedat}{1}h & =\frac{v_{y}^{2}}{2g}\\
& =\frac{0,36}{20}\\
& =1.8\times10^{-2}\mbox{m}
\end{alignedat}
$Jadi ketinggian maksimum dari tanah adalah $\left(H+1,8\times10^{-2}\right)\mbox{m}.$
SalahKecepatan balok di puncak bidang miring adalah
$\begin{alignedat}{1}v_{0} & =\sqrt{\frac{kd^{2}}{m}}\\
& =\sqrt{\frac{400\times0,05^{2}}{1}}\\
& =1\mbox{ ms}^{-1}
\end{alignedat}
$Kecepatan balok pada komponen vertikal adalah $v_{y}=v_{0}\mbox{sin 37}=0,6\mbox{ ms}^{-1}$
Ketinggian maskimum balok akibat komonen kecepatan ini adalah
$\begin{alignedat}{1}h & =\frac{v_{y}^{2}}{2g}\\
& =\frac{0,36}{20}\\
& =1.8\times10^{-2}\mbox{m}
\end{alignedat}
$Jadi ketinggian maksimum dari tanah adalah $\left(H+1,8\times10^{-2}\right)\mbox{m}.$
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Balok bermassa $m$ dilontarkan dari bidang miring dengan menggunakan pegas dengan kontanta $k$. Pegas dimampatkan sebesar $d$ kemudian dilepaskan (perhatikan gambar) sehingga balok tepat terlempar dari puncak bidang miring. Jika kemiringan bidang $\alpha$. Waktu yang dibutuhkan balok untuk menempuh jarak maksimum $(R)$ adalah… .
 Betul
BetulKecepatan balok di puncak bidang miring adalah $v_{0}=\sqrt{\frac{kd^{2}}{m}}$
Kecepatan balok pada komponen vertikal adalah $v_{0y}=\sqrt{\frac{kd^{2}}{m}}\mbox{sin}\alpha$
Waktu yang dibutuhkan balok dari O ke P adalah $t_{op}=\frac{1}{g}\sqrt{\frac{kd^{2}}{m}}\mbox{sin}\alpha$
Waktu yang dibutuhkan balok dari P ke S adalah $t_{ps}=\sqrt{\frac{2h_{p}}{g}}$ $=\sqrt{\frac{2}{g}\left(H+\frac{v_{0y}^{2}}{2g}\right)}$ $=\frac{1}{g}\sqrt{2\left(Hg+\frac{kd^{2}}{2m}\mbox{sin}^{2}\alpha\right)}$
Waktu yang dibutuhkan balok dari O ke S adalah $t_{os}=$$\frac{1}{g}\sqrt{\frac{kd^{2}}{m}\mbox{sin}\alpha}+\sqrt{2\left(gH+\frac{kd^{2}}{2m}\mbox{sin}^{2}\alpha\right)}$
 Salah
SalahKecepatan balok di puncak bidang miring adalah $v_{0}=\sqrt{\frac{kd^{2}}{m}}$
Kecepatan balok pada komponen vertikal adalah $v_{0y}=\sqrt{\frac{kd^{2}}{m}}\mbox{sin}\alpha$
Waktu yang dibutuhkan balok dari O ke P adalah $t_{op}=\frac{1}{g}\sqrt{\frac{kd^{2}}{m}}\mbox{sin}\alpha$
Waktu yang dibutuhkan balok dari P ke S adalah $t_{ps}=\sqrt{\frac{2h_{p}}{g}}$ $=\sqrt{\frac{2}{g}\left(H+\frac{v_{0y}^{2}}{2g}\right)}$ $=\frac{1}{g}\sqrt{2\left(Hg+\frac{kd^{2}}{2m}\mbox{sin}^{2}\alpha\right)}$
Waktu yang dibutuhkan balok dari O ke S adalah $t_{os}=$$\frac{1}{g}\sqrt{\frac{kd^{2}}{m}\mbox{sin}\alpha}+\sqrt{2\left(gH+\frac{kd^{2}}{2m}\mbox{sin}^{2}\alpha\right)}$

-
Pertanyaan ke 4 dari 5
4. Pertanyaan
Pegas A memiliki konstanta sebesar $k$ dan pegas B memiliki konstanta pegas sebesar $3k$ maka. Kedua pegas diregangkan sejauh $d$. Maka… .
BetulSemakin besar konstanta pegas maka semakin besar energi yang dibutuhkan untuk meregangkan pegas.
SalahSemakin besar konstanta pegas maka semakin besar energi yang dibutuhkan untuk meregangkan pegas.
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Sistem pegas terdiri dari dua pegas seperti gambar berikut.

Titik diantara dua pegas ditabrak oleh partikel sehingga pegas menyimpang sejauh $x$. Energi potensial pegas pada saat titik tersebut tersimpang sejauh $x$ adalah… .
BetulPanjang akhir masing-masing pegas adalah $\sqrt{L^{2}+x^{2}}$, sehingga pertambahan panjang pegas adalah $\sqrt{L^{2}+x^{2}}-L$ Energi potensial masing-masing pegas adalah
$\begin{alignedat}{1}E_{p} & =\frac{1}{2}k\times\left(\Delta x\right)^{2}\\
& =\frac{1}{2}k\left(\sqrt{L^{2}+x^{2}}-L\right)^{2}\\
& =\frac{1}{2}k\left(x^{2}+2L^{2}-2L\sqrt{L^{2}+x^{2}}\right)\\
& =\frac{1}{2}kx^{2}+kL\left(L-\sqrt{L^{2}+x^{2}}\right)
\end{alignedat}
$Sehingga energi totalnya =$kx^{2}+2kL\left(L-\sqrt{L^{2}+x^{2}}\right).$
SalahPanjang akhir masing-masing pegas adalah $\sqrt{L^{2}+x^{2}}$, sehingga pertambahan panjang pegas adalah $\sqrt{L^{2}+x^{2}}-L$ Energi potensial masing-masing pegas adalah
$\begin{alignedat}{1}E_{p} & =\frac{1}{2}k\times\left(\Delta x\right)^{2}\\
& =\frac{1}{2}k\left(\sqrt{L^{2}+x^{2}}-L\right)^{2}\\
& =\frac{1}{2}k\left(x^{2}+2L^{2}-2L\sqrt{L^{2}+x^{2}}\right)\\
& =\frac{1}{2}kx^{2}+kL\left(L-\sqrt{L^{2}+x^{2}}\right)
\end{alignedat}
$Sehingga energi totalnya =$kx^{2}+2kL\left(L-\sqrt{L^{2}+x^{2}}\right).$