Kamu dapat download modul & kumpulan soal besaran gerak melingkar dalam bentuk pdf pada link dibawah ini:

• Modul Besaran Gerak Melingkar
• Kumpulan Soal Mudah, Sedang & Sukar

Definisi Besaran Gerak Melingkar

Pengertian besaran gerak melingkar adalah gerak dengan lintasan melingkar.

1. Besaran Besaran Gerak Melingkar

Sebelum mempelajari gerak melingkar dalam kehidupan sehari-hari lebih detail, kita harus mengenal besaran besaran fisika yang berkaitan dengan gerak melingkar fisika. Jika sebuah objek bergerak melingkar maka objek selalu berjarak sama pada satu titik, sehingga harus ada besaran yang lain untuk menjelaskam posisi objek.

Besaran tersebut adalah posisi sudut. Posisi sudut (disimbolkan dengan $\theta$) biasanya diukur dari sumbu $x$ positif berlawanan arah gerak jarum jam. Jika sebuah objek bergerak melingkar dengan jari-jari $r$ maka pada saat $t$ tertentu, posisi objek di titik P adalah $(r,\theta)$.

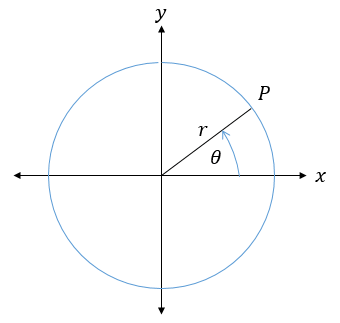
Posisi sudut diukur dalam radian (rad) diamana satu lingkaran penuh besarnya sama dengan $2\pi$ radian sehingga $\pi$ rad = $180^{\circ}.$

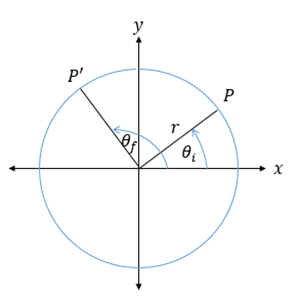
Jika objek berada dititik $P$ dengan posisi sudut awal $\theta_{i}$ kemudian objek berada di titik $P’$ dengan posisi sudut $\theta_{f}$ maka perubahan posisi sudut objek adalah $\Delta\theta=\theta_{f}-\theta_{i.}$. Perubahan posisi sudut persatuan waktu disebut dengan kecepatan sudut rata-rata ($\vec{\omega}$).

\begin{equation}
\vec{\omega}=\frac{\Delta\theta}{\Delta t}=\frac{\theta_{f}-\theta_{i}}{t_{f}-t_{i}}
\end{equation}

dengan $t_{f}$ dan $t_{i}$ adalah waktu untuk posisi akhir dan posisi awal.

Persamaan (1) menjelaskan kecepatan sudut untuk rentang waktu $\Delta t$ yang besar, jika $\Delta t$ sangat kecil atau mendekati nol, maka kecepatan sudut rata-rata disebut sebagai kecepatan sudut sesaat (kecepatan sudut) dapat dituliskan sebagai berikut.

\begin{eqnarray}
\omega & = & \lim_{\Delta t\rightarrow0}\frac{\Delta\theta}{\Delta t}=\frac{d\theta}{dt}
\end{eqnarray}

Sehingga dari persamaan (2) dapat disimpulkan bahwa kecepatan sudut merupakan turunan pertama fungsi posisi sudut terhadap waktu.

Selanjutnya gerak melingkar yang kecepatan sudutnya berubah setiap detik, perubahan kecepatan sudut setiap detik disebut dengan percepatan sudut rata-rata ($\alpha$).

\begin{equation}
\alpha=\frac{\Delta\omega}{\Delta t}=\frac{\omega_{f}-\omega_{i}}{t_{f}-t_{i}}
\end{equation}

Untuk selang waktu $\Delta t$ sangat kecil atau mendekati nol, percepatan sudut rata-rata disebut sebagai percepatan sudut sesaat (atau percepatan sudut) dituliskan sebagai berikut.

\begin{eqnarray}
\alpha & = & \lim_{\Delta t\rightarrow0}\frac{\Delta\omega}{\Delta t}=\frac{d\omega}{dt}
\end{eqnarray}

Sehingga dari persamaan (4) dapat disimpulkan bahwa kecepatan sudut merupakan turunan pertama fungsi kecepatan sudut terhadap waktu.

Berdasarkan persamaan (2), hubungan antara posisi sudut dengan kecepatan sudut dapat diperjelas sebagai berikut.

\begin{eqnarray}
\omega & = & \frac{d\theta}{dt}\nonumber \\
d\theta & = & \omega\, dt\nonumber \\
\intop_{\theta_{i}}^{\theta_{f}}d\theta & = & \intop\omega\, dt\nonumber \\
\theta_{f} & = & \theta_{i}+\intop\omega\, dt
\end{eqnarray}

Kemudian hubungan antara kecepatan sudut dengan percepatan sudut adalah sebagai berikut.

\begin{eqnarray}
\alpha & = & \frac{d\omega}{dt}\nonumber \\
d\omega & = & \alpha\, dt\nonumber \\
\intop_{\omega_{i}}^{\omega_{f}}d\omega & = & \intop\alpha\, dt\nonumber \\
\omega_{f} & = & \omega_{i}+\intop\alpha\, dt
\end{eqnarray}

Hubungan antara posisi sudut dengan percepatan sudut dapat diperoleh dengan memasukan persamaan (2) ke persamaan (4).

\begin{eqnarray}
\alpha & = & \frac{d\omega}{dt}\nonumber \\
& = & \frac{d}{dt}\frac{d\theta}{dt}\nonumber \\
& = & \frac{d^{2}\theta}{dt^{2}}
\end{eqnarray}

Berdasarkan persmaan (7) maka dapat disimpulkan bahwa percepatan sudut merupakan turunan kedua fungsi posisi sudut terhadap waktu.

Selain besaran-besaran tersebut, ada beberapa besaran fisika yang berkaitan dengan gerak melingkar, yaitu periode dan frekuensi.

Periode didefinisikan sebagai waktu yang dibutuhkan untuk melakukan satu kali putaran. Jika dalam waktu $t$ objek berputar sebanyak $n$ maka periode ($T$) dituliskan sebagai $T=\frac{t}{n}$. Sedangkan frekuensi ($f$) merupakan jumlah putaran tiap detik. Sehingga dirumuskan sebagai $f=\frac{n}{t}$. Hubungan kedua besaran ini adalah

\begin{eqnarray}
T & = & \frac{1}{f}
\end{eqnarray}

Jika objek telah berputar sebanyak $n$ kali maka sudut yang yang telah ditempuh adalah sebesar $\theta=2\pi n=\omega t$. Karena $f=\frac{n}{t}$ maka diperoleh hubungan antara kecepatan sudut dengan frekuensi dan periode sebagai berikut.

\begin{eqnarray}
2\pi n & = & \omega t\nonumber \\
\frac{2\pi n}{t} & = & \omega\nonumber \\
2\pi f & = & \omega\\
\frac{2\pi}{T} & = & \omega
\end{eqnarray}

2. Hubungan Gerak Melingkar & Gerak Translasi

Untuk memahami pengertian gerak translasi dan rotasi dalam Fisika terlebih dahulu kita akan mempelajari hubungannya dengan objek yang bergerak melingkar. Dalam hal ini gerak melingkar memiliki hubungan yang sangat erat dengan gerak translasi (gerak lurus).

Jika sebuah objek bergerak melingkar pada lintasan berjari-jari $r$ sehingga mengalami perubahan posisi sudut $\Delta\theta$ maka jarak yang ditempuh ($\Delta s$) oleh objek tersebut adalah jari-jari dikalikan dengan perubahan sudut.

\begin{eqnarray}
\Delta s & = & r\Delta\theta
\end{eqnarray}

Sehinga kelajuan objek atau kecepatan linear objek dapat ditentukan sebagai berikut.

\begin{eqnarray}
v & = & \frac{\Delta s}{\Delta t}\nonumber \\
v & = & \frac{r\Delta\theta}{\Delta t}\nonumber \\
v & = & r\omega
\end{eqnarray}

dengan cara yang analog maka hubungan antara percepatan linear dan percepatan sudut dapat dituliskan sebagai berikut.

\begin{eqnarray}
a & = & \frac{\Delta v}{\Delta t}\nonumber \\
a & = & \frac{r\Delta\omega}{\Delta t}\nonumber \\
a & = & r\alpha
\end{eqnarray}

Kecepatan linear dan percepatan linear memliki arah tegak lurus terhadap jari-jarinya atau searah dengan garis singgung lingkaran. Sehingga arah kecepatan di setiap titik lintasan selalu berubah-ubah. Hal inilah yang mengakibatkan kecepatan pada gerak melingkar selalu berubah-ubah, meskipun pada gerak melingkar dengan kelajuan tetap. Kecepatan linear dan percepatan linear juga disebut sebagai kecepatan dan percepatan tangensial.

Arah kecepatan yang berubah-ubah di setiap titik disebabkan oleh adanya percepatan sentripetal. Untuk memahami adanya percepatan sentripetal ini, dapat ditinjau dari sebuah gerak melingkar dengan kelajuan konstan. Perhatikan gambar berikut.

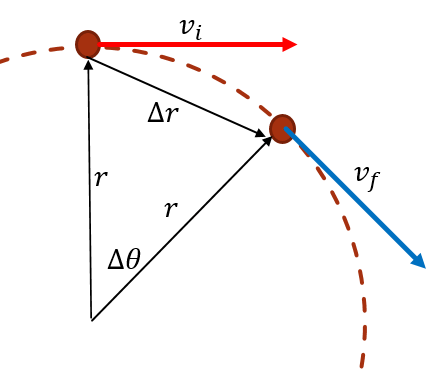
Jika sebuah partikel bergerak melingkar menempuh sudut sebesar $\Delta\theta,$ dengan kecepatan di dua titik $v_{i}$ dan $v_{f}$ besarnya sama sebesar $v.$ Dari gambar di atas maka dapat dibentuk penjumlahan vektor kecepatan dengan metode grafis seperti gambar berikut.

Dari kedua gambar tersebut maka diperoleh hubungan $\frac{\Delta v}{v}=\frac{\Delta r}{r}$ atau $\Delta v=\frac{\Delta r}{r}v.$ Sehingga percepatan sentripetal dapat dituliskan sebagai berikut.

\begin{eqnarray}
a & = & \frac{\Delta v}{\Delta t}\nonumber \\
a & = & \frac{1}{\Delta t}\frac{\Delta r}{r}v\nonumber \\
a & = & \frac{v^{2}}{r}
\end{eqnarray}

Contoh Soal dan Pembahasan Besaran Gerak Melingkar

1. Posisi sebuah partikel yang bergerak melingkar dinyatakan sebagai fungsi posisi $\theta(t)=12t^{2}-8t+20$ rad. Tentukan:
   a. kecepatan sudut rata-rata untuk rentang $t=0$ s hingga $t=2$ s!
   b. kecepatan sudut saat $t=2$ s.!
   c. percepatan sudut!

Penyelesaian:

Posisi sudut untuk masing-masing $t$ tersebut adalah
$\begin{alignedat}{1}\theta(t) & =12t^{2}-8t+20\mbox{ rad}\\
\theta(0) & =0-0+20\mbox{ rad}\\
& =20\mbox{ rad}\\
\theta(2) & =12(4)-8(2)+20\mbox{ rad}\\
& =24-16+20\mbox{ rad}\\
& =28\mbox{ rad}
\end{alignedat}
$

Sehingga kecepatan sudut rata-ratanya adalah
$\begin{alignedat}{1}\vec{\omega} & =\frac{28-20}{2-0}\\
& =4\mbox{ rad/s}
\end{alignedat}
$

2. Kecepatan sudut sesaat untuk $t=2$ s

$\begin{alignedat}{1}\omega(t) & =\frac{d\theta}{dt}\\
& =\frac{d}{dt}\left(12t^{2}-8t+20\right)\\
\omega(2) & =24t-8\\
& =48-8\\
& =40\mbox{ rad/s}
\end{alignedat}
$

3. Percepatan sudut

$\begin{alignedat}{1}\alpha(t) & =\frac{d\omega}{dt}\\
& =\frac{d}{dt}\left(24t-8\right)\\
\alpha(t) & =24\mbox{ rad/s}^{2}
\end{alignedat}
$