Ingin mempelajari rumus kuartil data berkelompok secara lebih mendalam? Kamu bisa menyimak baik-baik pembahasan dari video yang ada di sini. Setelahnya, kamu bisa mengerjakan kuis berupa latihan soal untuk mengasah kemampuan.
Di sini, kamu akan belajar tentang Kuartil Data Berkelompok melalui video yang dibawakan oleh Bapak Anton Wardaya. Kamu akan diajak untuk memahami materi hingga metode menyelesaikan soal.
Selain itu, kamu juga akan mendapatkan latihan soal interaktif dalam 3 tingkat kesulitan (mudah, sedang, sukar). Tentunya menarik, bukan? Penjelasan yang didapatkan bisa dipraktikkan secara langsung.
Sekarang, kamu bisa mulai belajar dengan 1 video dan 3 set latihan soal yang ada di halaman ini. Apabila materi ini berguna, bagikan ke teman atau rekan kamu supaya mereka juga mendapatkan manfaatnya.
Kamu dapat download modul & contoh soal serta kumpulan latihan soal lengkap dalam bentuk pdf pada list dibawah ini:
Kuartil Data Berkelompok
Latihan Soal Kuartil Data Berkelompok (Mudah)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Kuartil bawah dari data pada tabel dibawah ini adalah…
 Betul
BetulBanyaknya data
$\begin{aligned}(n) & =2+6+4+2\\
& =14
\end{aligned}
$$\begin{aligned}Q_{1} & =X_{\left(\frac{n+2}{4}\right)}\\
& =X_{\frac{14+2}{4}}\\
& =X_{4}
\end{aligned}
$Quartil bawah terletak pada data keempat, data keempat adalah $4.$
Jadi kuartil bawahnya adalah $4.$
SalahBanyaknya data
$\begin{aligned}(n) & =2+6+4+2\\
& =14
\end{aligned}
$$\begin{aligned}Q_{1} & =X_{\left(\frac{n+2}{4}\right)}\\
& =X_{\frac{14+2}{4}}\\
& =X_{4}
\end{aligned}
$Quartil bawah terletak pada data keempat, data keempat adalah $4.$
Jadi kuartil bawahnya adalah $4.$
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Pada tabel berikut diperlihatkan nilai ulangan $50$ siswa.

Dari data itu berturut-turut diperoleh…
Betul$2+4+12+a$$+11+8+1=50$
$a+38=50$
$a=12$
$\begin{aligned}Q_{2} & =\frac{1}{2}\left(x_{\frac{50}{2}}+x_{\left(\frac{50}{2}+1\right)}\right)\\
& =\frac{x_{25}+x_{26}}{2}
\end{aligned}
$data ke 25 dan ke 26 adalah sama- sama $7.$
$\begin{aligned}Q_{2} & =\frac{7+7}{2}\\
& =7
\end{aligned}
$Modusnya adalah $6$ dan $7$ karena memiliki frekuensi yang sama banyak yaitu $12.$
Salah$2+4+12+a$$+11+8+1=50$
$a+38=50$
$a=12$
$\begin{aligned}Q_{2} & =\frac{1}{2}\left(x_{\frac{50}{2}}+x_{\left(\frac{50}{2}+1\right)}\right)\\
& =\frac{x_{25}+x_{26}}{2}
\end{aligned}
$data ke 25 dan ke 26 adalah sama- sama $7.$
$\begin{aligned}Q_{2} & =\frac{7+7}{2}\\
& =7
\end{aligned}
$Modusnya adalah $6$ dan $7$ karena memiliki frekuensi yang sama banyak yaitu $12.$
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Perhatikan tabel berikut ini :

Nilai kuartil atas dari data tersebut adalah…
BetulUkuran data :
$n=7+7+9+10$$+12+8+7$
$=60$
$\begin{aligned}Q_{3} & =x_{\frac{1}{4}\left(3n+2\right)}\\
& =x_{\frac{1}{4}(180+2)}\\
& =x_{45\frac{1}{2}}
\end{aligned}
$$\begin{aligned}Q_{3} & =x_{45}+\frac{1}{2}\left(x_{46}-x_{45}\right)\\
& =162+\frac{1}{2}\left(165-162\right)\\
& =162+1,5\\
& =163,5.
\end{aligned}
$SalahUkuran data :
$n=7+7+9+10$$+12+8+7$
$=60$
$\begin{aligned}Q_{3} & =x_{\frac{1}{4}\left(3n+2\right)}\\
& =x_{\frac{1}{4}(180+2)}\\
& =x_{45\frac{1}{2}}
\end{aligned}
$$\begin{aligned}Q_{3} & =x_{45}+\frac{1}{2}\left(x_{46}-x_{45}\right)\\
& =162+\frac{1}{2}\left(165-162\right)\\
& =162+1,5\\
& =163,5.
\end{aligned}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Kuartil bawah dari data berikut adalah…
 Betul
Betul
Banyaknya data $(n)=80$
Letak kuartil bawah $=\frac{1}{4}n$$=\frac{1}{4}(80)$$=20$
Letak kuartil bawah berada pada kelas kedua yaitu pada selang $61-70.$
$\begin{aligned}Q_{1} & =tb+p\left(\frac{\frac{1}{4}n-fk}{f}\right)\\
& =60,5+10\left(\frac{20-8}{16}\right)\\
& =60,5+10\left(\frac{12}{16}\right)\\
& =60,5+7,5\\
& =68.
\end{aligned}
$Salah
Banyaknya data $(n)=80$
Letak kuartil bawah $=\frac{1}{4}n$$=\frac{1}{4}(80)$$=20$
Letak kuartil bawah berada pada kelas kedua yaitu pada selang $61-70.$
$\begin{aligned}Q_{1} & =tb+p\left(\frac{\frac{1}{4}n-fk}{f}\right)\\
& =60,5+10\left(\frac{20-8}{16}\right)\\
& =60,5+10\left(\frac{12}{16}\right)\\
& =60,5+7,5\\
& =68.
\end{aligned}
$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
Diketahui daftar distribusi nilai matematika sebagai berikut :

Nilai kuartil atas adalah…
Betul
Letak kuartil atas
$\begin{aligned}\left(Q_{3}\right) & =\frac{3}{4}n\\
& =\frac{3}{4}(40)\\
& =30
\end{aligned}
$Kuartil atas terletak pada kelas keempat pada interval $30-34.$
$\begin{aligned}Q_{3} & =tb+p\left(\frac{\frac{3}{4}n-fk}{f}\right)\\
& =29,5+5\left(\frac{30-20}{13}\right)\\
& =29,5+\frac{50}{13}\\
& =29,5+3,85\\
& =33,35.
\end{aligned}
$Salah
Letak kuartil atas
$\begin{aligned}\left(Q_{3}\right) & =\frac{3}{4}n\\
& =\frac{3}{4}(40)\\
& =30
\end{aligned}
$Kuartil atas terletak pada kelas keempat pada interval $30-34.$
$\begin{aligned}Q_{3} & =tb+p\left(\frac{\frac{3}{4}n-fk}{f}\right)\\
& =29,5+5\left(\frac{30-20}{13}\right)\\
& =29,5+\frac{50}{13}\\
& =29,5+3,85\\
& =33,35.
\end{aligned}
$
Latihan Soal Kuartil Data Berkelompok (Sedang)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Perhatikan tabel berikut :

Simpangan kuartil dari tabel diatas adalah…
Betul
Letak $Q_{1}=\frac{1}{4}n=\frac{1}{4}.60=15$ (berada di kelas kedua)
$\begin{aligned}Q_{1} & =tb+p\left(\frac{\frac{1}{4}n-fk_{1}}{f_{1}}\right)\\
& =54,5+5\left(\frac{15-7}{10}\right)\\
& =54,5+4\\
& =58,5
\end{aligned}
$Letak $Q_{3}=\frac{3}{4}n=\frac{3}{4}.60=45$(berada di kelas keempat)
$\begin{aligned}Q_{3} & =tb+p\left(\frac{\frac{3}{4}n-fk_{3}}{f_{3}}\right)\\
& =64,5+5\left(\frac{45-38}{18}\right)\\
& =64,5+1,94\\
& =66,44
\end{aligned}
$Simpangan kuartil $=\frac{1}{2}\left(Q_{3}-Q_{1}\right)$
$=\frac{1}{2}(66,44-58,5)$
$=\frac{1}{2}\left(7,94\right)$
$=3,972.$
Salah
Letak $Q_{1}=\frac{1}{4}n=\frac{1}{4}.60=15$ (berada di kelas kedua)
$\begin{aligned}Q_{1} & =tb+p\left(\frac{\frac{1}{4}n-fk_{1}}{f_{1}}\right)\\
& =54,5+5\left(\frac{15-7}{10}\right)\\
& =54,5+4\\
& =58,5
\end{aligned}
$Letak $Q_{3}=\frac{3}{4}n=\frac{3}{4}.60=45$(berada di kelas keempat)
$\begin{aligned}Q_{3} & =tb+p\left(\frac{\frac{3}{4}n-fk_{3}}{f_{3}}\right)\\
& =64,5+5\left(\frac{45-38}{18}\right)\\
& =64,5+1,94\\
& =66,44
\end{aligned}
$Simpangan kuartil $=\frac{1}{2}\left(Q_{3}-Q_{1}\right)$
$=\frac{1}{2}(66,44-58,5)$
$=\frac{1}{2}\left(7,94\right)$
$=3,972.$
-
Pertanyaan ke 2 dari 5
2. Pertanyaan
Diketahui distribusi nilai dari $36$ murid sebagai berikut :

Jika rata-ratanya adalah 6, maka nilai kuartil tengah adalah…
Betul$\begin{aligned}3+4+x+7+y+5+4 & =36\\
x+y+23 & =36\\
x+y & =13
\end{aligned}
$$x=13-y….(1)$
Rata-rata dari $36$ siswa adalah $6$ sehingga :
$\begin{aligned}\overline{x} & =\frac{3\cdot3+4\cdot4+5x+6\cdot7+7y+8\cdot5+9\cdot4}{36}\\
& =\frac{9+16+5x+42+7y+40+36}{36}\\
6 & =\frac{143+5x+7y}{36}\\
216 & =143+5x+7y
\end{aligned}
$$5x+7y=73…..(2)$
Substitusikan pers (1) ke pers (2) sehingga diperoleh :
$5\left(13-y\right)+7y=73$
$65-5y+7y=73$
$2y=73-65=8$
$y=4$
Substitusikan nilai y = 4 ke pers (1) sehingga diperoleh nilai x = 9

$Q_{2}=\frac{1}{2}\left(x_{18}+x_{19}\right)$
$x_{18}=6$ dan $x_{19}=6$
$\begin{aligned}Q_{2} & =\frac{1}{2}\left(6+6\right)\\
& =6
\end{aligned}
$Jadi kuartil tengah dari tabel diatas adalah $6.$
Salah$\begin{aligned}3+4+x+7+y+5+4 & =36\\
x+y+23 & =36\\
x+y & =13
\end{aligned}
$$x=13-y….(1)$
Rata-rata dari $36$ siswa adalah $6$ sehingga :
$\begin{aligned}\overline{x} & =\frac{3\cdot3+4\cdot4+5x+6\cdot7+7y+8\cdot5+9\cdot4}{36}\\
& =\frac{9+16+5x+42+7y+40+36}{36}\\
6 & =\frac{143+5x+7y}{36}\\
216 & =143+5x+7y
\end{aligned}
$$5x+7y=73…..(2)$
Substitusikan pers (1) ke pers (2) sehingga diperoleh :
$5\left(13-y\right)+7y=73$
$65-5y+7y=73$
$2y=73-65=8$
$y=4$
Substitusikan nilai y = 4 ke pers (1) sehingga diperoleh nilai x = 9

$Q_{2}=\frac{1}{2}\left(x_{18}+x_{19}\right)$
$x_{18}=6$ dan $x_{19}=6$
$\begin{aligned}Q_{2} & =\frac{1}{2}\left(6+6\right)\\
& =6
\end{aligned}
$Jadi kuartil tengah dari tabel diatas adalah $6.$
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
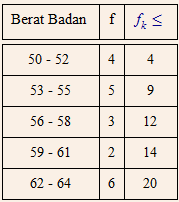
Quartil ketiga dari data berikut adalah…
 Betul
BetulBanyaknya data
$n=4+5+3$$+2+6$$=20$
Letak kuartil atas$=\frac{3}{4}n$$=\frac{3}{4}(20)$$=15$
Letak kuartil atas berada pada data ke $15$

Kuartil berada pada kelas kelima.
$\begin{aligned}Q_{3} & =tb+p\left(\frac{\frac{3}{4}n-fk}{f}\right)\\
& =61,5+3\left(\frac{15-14}{6}\right)\\
& =61,5+0,5\\
& =62.
\end{aligned}
$SalahBanyaknya data
$n=4+5+3$$+2+6$$=20$
Letak kuartil atas$=\frac{3}{4}n$$=\frac{3}{4}(20)$$=15$
Letak kuartil atas berada pada data ke $15$

Kuartil berada pada kelas kelima.
$\begin{aligned}Q_{3} & =tb+p\left(\frac{\frac{3}{4}n-fk}{f}\right)\\
& =61,5+3\left(\frac{15-14}{6}\right)\\
& =61,5+0,5\\
& =62.
\end{aligned}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Jangkauan kuartil dari tabel dibawah ini adalah…
 Betul
BetulBanyaknya data
$(n)=4+6+7$$+10+3+2$$=32$
Letak Kuartil bawah $=\frac{1}{4}n$$=\frac{1}{4}(32)$$=8$
kelas kuartil bawah berada pada kelas kedua
Letak kuartil atas $=\frac{3}{4}n$$=\frac{3}{4}(32)$$=24$
letak kuartil atas berada pada kelas keempat

$\begin{aligned}Q_{1} & =tb+p\left(\frac{\frac{1}{4}n-fk}{f}\right)\\
& =5,5+5\left(\frac{8-4}{6}\right)\\
& =5,5+3,33\\
& =8,83
\end{aligned}
$$\begin{aligned}Q_{3} & =tb+p\left(\frac{\frac{3}{4}n-fk}{f}\right)\\
& =15,5+5\left(\frac{24-17}{10}\right)\\
& =15,5+3,5\\
& =19
\end{aligned}
$Jangkauan kuartil $=Q_{3}-Q_{1}$$=19-8,83$$=10,17.$
SalahBanyaknya data
$(n)=4+6+7$$+10+3+2$$=32$
Letak Kuartil bawah $=\frac{1}{4}n$$=\frac{1}{4}(32)$$=8$
kelas kuartil bawah berada pada kelas kedua
Letak kuartil atas $=\frac{3}{4}n$$=\frac{3}{4}(32)$$=24$
letak kuartil atas berada pada kelas keempat

$\begin{aligned}Q_{1} & =tb+p\left(\frac{\frac{1}{4}n-fk}{f}\right)\\
& =5,5+5\left(\frac{8-4}{6}\right)\\
& =5,5+3,33\\
& =8,83
\end{aligned}
$$\begin{aligned}Q_{3} & =tb+p\left(\frac{\frac{3}{4}n-fk}{f}\right)\\
& =15,5+5\left(\frac{24-17}{10}\right)\\
& =15,5+3,5\\
& =19
\end{aligned}
$Jangkauan kuartil $=Q_{3}-Q_{1}$$=19-8,83$$=10,17.$
-
Pertanyaan ke 5 dari 5
5. Pertanyaan
Rataan kuartil pada tabel berikut adalah…
 Betul
Betul
Letak $Q1=\frac{1}{4}n=\frac{1}{4}\cdot20=5$ (berada di kelas kedua)
$\begin{aligned}Q_{1} & =35,5+5\left(\frac{5-2}{4}\right)\\
& =35,5+3,75\\
& =39,25
\end{aligned}
$Letak $Q_{2}=\frac{2}{4}n=\frac{2}{4}\cdot20=10$ (berada di kelas ke tiga)
$\begin{aligned}Q_{2} & =40,5+5\left(\frac{10-6}{8}\right)\\
& =40,5+2,5\\
& =43
\end{aligned}
$Letak $Q_{3}=\frac{3}{4}n=\frac{3}{4}\cdot20=15$ (berada di kelas empat)
$\begin{aligned}Q_{3} & =45,5+5\left(\frac{15-14}{5}\right)\\
& =45,5+1\\
& =46,5
\end{aligned}
$Rataan kuartil $=\frac{1}{2}\left(Q_{1}+Q_{3}\right)$$=\frac{85,75}{2}$$=42,875.$
Salah
Letak $Q1=\frac{1}{4}n=\frac{1}{4}\cdot20=5$ (berada di kelas kedua)
$\begin{aligned}Q_{1} & =35,5+5\left(\frac{5-2}{4}\right)\\
& =35,5+3,75\\
& =39,25
\end{aligned}
$Letak $Q_{2}=\frac{2}{4}n=\frac{2}{4}\cdot20=10$ (berada di kelas ke tiga)
$\begin{aligned}Q_{2} & =40,5+5\left(\frac{10-6}{8}\right)\\
& =40,5+2,5\\
& =43
\end{aligned}
$Letak $Q_{3}=\frac{3}{4}n=\frac{3}{4}\cdot20=15$ (berada di kelas empat)
$\begin{aligned}Q_{3} & =45,5+5\left(\frac{15-14}{5}\right)\\
& =45,5+1\\
& =46,5
\end{aligned}
$Rataan kuartil $=\frac{1}{2}\left(Q_{1}+Q_{3}\right)$$=\frac{85,75}{2}$$=42,875.$
Latihan Soal Kuartil Data Berkelompok (Sukar)
Ringkasan kuis
0 dari 5 pertanyaan telah diselesaikan
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
Informasi
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
Anda harus masuk atau mendaftar untuk memulai kuis.
Anda harus menyelesaikan kuis dibawah ini, untuk memulai kuis ini:
Hasil
Hasil
0 dari 5 pertanyaan terjawab dengan benar
Waktu yang telah berlalu
Kategori
- Tidak Berkategori 0%
- 1
- 2
- 3
- 4
- 5
- Terjawab
- Tinjau
-
Pertanyaan ke 1 dari 5
1. Pertanyaan
Nilai dari $20$ siswa tampak pada tabel berikut :

Jika kuartil tengah $Q_{2}=66,1,$ maka nilai kuartil atasnya adalah…
BetulKelas median = $Q_{2}$ berada kelas ketiga
$\begin{aligned}Q_{2} & =tb+p\left(\frac{\frac{1}{2}n-fk_{2}}{f_{2}}\right)\\
66,1 & =65,5+3\left(\frac{\frac{1}{2}\cdot20-(6+a)}{5}\right)\\
0,6 & =3\left(\frac{10-6-a}{5}\right)\\
\frac{0,6\times5}{3} & =4-a\\
1 & =4-a\\
a & =3
\end{aligned}
$Karena banyaknya data adalah $20,$ maka :
$\begin{aligned}6+a+5+b+1 & =20\\
6+3+5+b+1 & =20\\
b+15 & =20\\
b & =5
\end{aligned}
$Jadi diperoleh nilai $a=3$ dan $b=5$
Letak kuartil atas $=\frac{3}{4}\cdot20=15$
Letak kuartil atas berada di kelas ke 4

$\begin{aligned}Q_{3} & =tb+p\left(\frac{\frac{3}{4}n-fk_{3}}{f_{3}}\right)\\
& =68,5+3\left(\frac{15-14}{5}\right)\\
& =68,5+\frac{3}{5}\\
& =68,5+0,6\\
& =69,1.
\end{aligned}
$SalahKelas median = $Q_{2}$ berada kelas ketiga
$\begin{aligned}Q_{2} & =tb+p\left(\frac{\frac{1}{2}n-fk_{2}}{f_{2}}\right)\\
66,1 & =65,5+3\left(\frac{\frac{1}{2}\cdot20-(6+a)}{5}\right)\\
0,6 & =3\left(\frac{10-6-a}{5}\right)\\
\frac{0,6\times5}{3} & =4-a\\
1 & =4-a\\
a & =3
\end{aligned}
$Karena banyaknya data adalah $20,$ maka :
$\begin{aligned}6+a+5+b+1 & =20\\
6+3+5+b+1 & =20\\
b+15 & =20\\
b & =5
\end{aligned}
$Jadi diperoleh nilai $a=3$ dan $b=5$
Letak kuartil atas $=\frac{3}{4}\cdot20=15$
Letak kuartil atas berada di kelas ke 4

$\begin{aligned}Q_{3} & =tb+p\left(\frac{\frac{3}{4}n-fk_{3}}{f_{3}}\right)\\
& =68,5+3\left(\frac{15-14}{5}\right)\\
& =68,5+\frac{3}{5}\\
& =68,5+0,6\\
& =69,1.
\end{aligned}
$ -
Pertanyaan ke 2 dari 5
2. Pertanyaan
Untuk memudahkan perhitungan, semua nilai pengamatan dikurangi $1300,$ nilai baru menghasilkan jangkauan $28,$ rata-rata 11,7 , simpangan kuartil $7,4$ dan modus $12.$ data asli mempunyai…
i. Rata-rata $1311,7$
ii. Jangkauan$=28$
iii. Modus $=28$
iv. Simpangan Kuartil $=657,4$BetulMisalkan data aslinya diurutkan adalah :
$x_{1},\, x_{2},\, x_{3},\,…,\, x_{n}$
Rata-rata $=\frac{x_{1}+x_{2}+x_{3}…+x_{n}}{n}$
Semua nilai dikurangi $1300,$ rata-rata $11,7$
$11,7=\frac{\left(x_{1}-1300\right)+\left(x_{2}-1300\right)+\left(x_{3}-1300.\right)..+\left(x_{n}-1300\right)}{n}$
$11,7=\frac{x_{1}+x_{2}+x_{3}…+x_{n}-1300n}{n}=\mbox{ rata-rata }-1300$
Rata-rata $=1300+11,7=1311,7$
Modus $=12+1300=1312$
angkauan $=x_{n}-x_{1}$
Setelah dikurangi $1300$ jangkauannya $28$
$\left(x_{n}-1300\right)-\left(x_{1}-1300\right)=28$
$x_{n}-x_{1}=28$ (jangkauan asli)
Simpangan kuartil setelah data dikurangi $1300,$ simpangan kuartilnya adalah $7,4$
$7,4=\frac{1}{2}\left\{ \left(Q_{3}-1300\right)-\left(Q_{1}-1300\right)\right\} $
$7,4=\frac{1}{2}\left(Q_{3}-Q_{1}\right)$ (simpangan data asli)
Jadi pernyataan yang benar adalah i dan ii .
SalahMisalkan data aslinya diurutkan adalah :
$x_{1},\, x_{2},\, x_{3},\,…,\, x_{n}$
Rata-rata $=\frac{x_{1}+x_{2}+x_{3}…+x_{n}}{n}$
Semua nilai dikurangi $1300,$ rata-rata $11,7$
$11,7=\frac{\left(x_{1}-1300\right)+\left(x_{2}-1300\right)+\left(x_{3}-1300.\right)..+\left(x_{n}-1300\right)}{n}$
$11,7=\frac{x_{1}+x_{2}+x_{3}…+x_{n}-1300n}{n}=\mbox{ rata-rata }-1300$
Rata-rata $=1300+11,7=1311,7$
Modus $=12+1300=1312$
angkauan $=x_{n}-x_{1}$
Setelah dikurangi $1300$ jangkauannya $28$
$\left(x_{n}-1300\right)-\left(x_{1}-1300\right)=28$
$x_{n}-x_{1}=28$ (jangkauan asli)
Simpangan kuartil setelah data dikurangi $1300,$ simpangan kuartilnya adalah $7,4$
$7,4=\frac{1}{2}\left\{ \left(Q_{3}-1300\right)-\left(Q_{1}-1300\right)\right\} $
$7,4=\frac{1}{2}\left(Q_{3}-Q_{1}\right)$ (simpangan data asli)
Jadi pernyataan yang benar adalah i dan ii .
-
Pertanyaan ke 3 dari 5
3. Pertanyaan
Sekumpulan data memiliki simpangan kuartil $4$ dan kuartil bawah $12.$ Jika setiap data ditambah a, kemudian dibagi b ternyata menghasilkan data baru dengan kuartil atas $56$ dan kuartil bawah adalah $40,$ maka nilai $a+4b=…$
BetulSimpangan kuartil 4, dan kuartil bawah 12, maka kuartil atas dapat kita cari
$Qd=\frac{1}{2}\left(Q_{3}-Q_{1}\right)$
$4=\frac{1}{2}\left(Q_{3}-12\right)$
$8=Q_{3}-12\Rightarrow Q_{3}=20$
Kuartil bawah $12,$ jika data ditambah a dan kemudian dibagi b, maka menjadi;
$40=\frac{12+a}{b}$$\Rightarrow40b-a=12…(1)$
Kuartil atas 30, jika data ditambah a dan kemudian dibagi b, maka menjadil
$56=\frac{20+a}{b}$$\Rightarrow56b-a=20….(2)$
Pers (2) kurangkan dengan pers (1) sehingga diperoleh :
$16b=8\Rightarrow b=\frac{1}{2}$
Substitusikan $b=\frac{1}{2}$ ke pers (1) :
$40\left(\frac{1}{2}\right)-a=12$
$20-a=12\Rightarrow a=8$
Jadi nilai
$\begin{aligned}a+4b & =8+4\left(\frac{1}{2}\right)\\
& =8+2\\
& =10.
\end{aligned}
$SalahSimpangan kuartil 4, dan kuartil bawah 12, maka kuartil atas dapat kita cari
$Qd=\frac{1}{2}\left(Q_{3}-Q_{1}\right)$
$4=\frac{1}{2}\left(Q_{3}-12\right)$
$8=Q_{3}-12\Rightarrow Q_{3}=20$
Kuartil bawah $12,$ jika data ditambah a dan kemudian dibagi b, maka menjadi;
$40=\frac{12+a}{b}$$\Rightarrow40b-a=12…(1)$
Kuartil atas 30, jika data ditambah a dan kemudian dibagi b, maka menjadil
$56=\frac{20+a}{b}$$\Rightarrow56b-a=20….(2)$
Pers (2) kurangkan dengan pers (1) sehingga diperoleh :
$16b=8\Rightarrow b=\frac{1}{2}$
Substitusikan $b=\frac{1}{2}$ ke pers (1) :
$40\left(\frac{1}{2}\right)-a=12$
$20-a=12\Rightarrow a=8$
Jadi nilai
$\begin{aligned}a+4b & =8+4\left(\frac{1}{2}\right)\\
& =8+2\\
& =10.
\end{aligned}
$ -
Pertanyaan ke 4 dari 5
4. Pertanyaan
Perhatikan gambar berikut!

Nilai kuartil tengah adalah…
BetulJika histogram diatas diubah kedalam distribusi frekuensi maka akan menjadi :

banyaknya data $(n)=48$
Letak kuartil tengah;
$\begin{aligned}\left(Q_{2}\right) & =\frac{2}{4}n\\
& =\frac{1}{2}(48)\\
& =24
\end{aligned}
$Letak kuartil tengah berada pada kelas ketiga
$Q_{2}=tb+p\left(\frac{\frac{2}{4}n-fk}{f}\right)$
$\begin{aligned}Q_{3} & =29,5+5\left(\frac{24-23}{15}\right)\\
& =29,5+\frac{1}{3}\\
& =29,5+0,33\\
& =29,83.
\end{aligned}
$SalahJika histogram diatas diubah kedalam distribusi frekuensi maka akan menjadi :

banyaknya data $(n)=48$
Letak kuartil tengah;
$\begin{aligned}\left(Q_{2}\right) & =\frac{2}{4}n\\
& =\frac{1}{2}(48)\\
& =24
\end{aligned}
$Letak kuartil tengah berada pada kelas ketiga
$Q_{2}=tb+p\left(\frac{\frac{2}{4}n-fk}{f}\right)$
$\begin{aligned}Q_{3} & =29,5+5\left(\frac{24-23}{15}\right)\\
& =29,5+\frac{1}{3}\\
& =29,5+0,33\\
& =29,83.
\end{aligned}
$ -
Pertanyaan ke 5 dari 5
5. Pertanyaan
Perhatikan gambar berikut!

Nilai kuartil atas adalah…
BetulJika gambar diatas diubah ke dalam tabel frekuensi akan menjadi :

Banyaknya data $(n)=24$
Letak kuartil atas$=\frac{3}{4}n$$=\frac{3}{4}(20)$$=15$
Letak kuartil atas berada pada kelas ketiga
tepi atas kelas kedua adalah$51$
$\begin{aligned}Q_{3} & =tb+p\left(\frac{\frac{3}{4}n-fk}{f}\right)\\
& =51+5\left(\frac{15-9}{6}\right)\\
& =51+5\\
& =56.
\end{aligned}
$SalahJika gambar diatas diubah ke dalam tabel frekuensi akan menjadi :

Banyaknya data $(n)=24$
Letak kuartil atas$=\frac{3}{4}n$$=\frac{3}{4}(20)$$=15$
Letak kuartil atas berada pada kelas ketiga
tepi atas kelas kedua adalah$51$
$\begin{aligned}Q_{3} & =tb+p\left(\frac{\frac{3}{4}n-fk}{f}\right)\\
& =51+5\left(\frac{15-9}{6}\right)\\
& =51+5\\
& =56.
\end{aligned}
$